Multifactorial Inheritance
Lynn B. Jorde
Although the genetics of most single-gene disorders are now quite well understood, these disorders account for a relatively small proportion of the total disease burden in the pediatric population compared with diseases that are thought to arise from the interaction of multiple genetic and environmental factors. Examples of the latter include neural tube defects, congenital heart defects, isolated cleft lip/palate, and clubfoot. Many multifactorial disorders are present at birth and are thus considered to be congenital malformations, but others, such as infantile autism and type 1 diabetes, typically present later in childhood. This section will review basic concepts relating to the genetics of multifactorial disorders, with emphasis on diseases that occur in the pediatric population.
THE MULTIFACTORIAL MODEL
Many quantitative traits, such as height, blood pressure, and IQ, exhibit a normal distribution in human populations, which is the consequence of multiple genetic and environmental influences on the phenotype (hence the designation multifactorial). Most of the diseases to be considered in this chapter, however, are either present or absent in the individual. There is an underlying liability distribution for these disorders, which follows the familiar bell-shaped curve. If an individual has enough liability factors to exceed a threshold, then that person is affected with the disorder (Fig. 171-1).
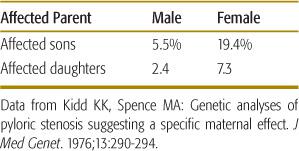
In some cases, the threshold may be higher in one sex than in the other. Pyloric stenosis is a classic example of a multifactorial disease that appears to follow such a sex-specific threshold model. This birth defect, in which a narrowing of the pylorus produces constipation, chronic vomiting, weight loss, and electrolyte imbalance, affects approximately 1 in 1000 females and approximately 1 in 200 males. This pattern indicates that the liability threshold is higher for females than for males. Accordingly, affected females should possess more liability factors than should affected males. Having more risk factors, affected females will be more likely to produce affected offspring. This prediction is borne out in Table 171-1, which shows that the recurrence risk is considerably higher for the offspring of affected females than for the offspring of affected males.
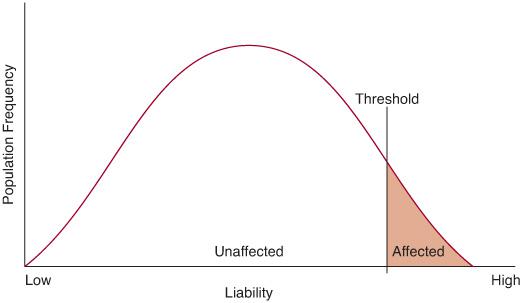
FIGURE 171-1. The liability distribution for a multifactorial disease. An individual must exceed a threshold on this distribution to be affected with the disease.
A similar pattern is seen in infantile autism, in which the male-to-female ratio is approximately 4:1. The threshold is thought to be higher for females than males in this multifactorial disorder, and one large study showed that the recurrence risk for siblings of affected females is twice as high as the risk for siblings of affected males (7.0% versus 3.5%).
RECURRENCE RISKS FOR MULTIFACTORIAL DISEASES
Recurrence risks for single-gene diseases are known with considerable certainty (50% for an autosomal-dominant disease and 25% for an autosomal-recessive disease, although incomplete penetrance may decrease these figures). In contrast, the number of genetic and environmental factors (not to mention their identity) is unknown for most multifactorial disorders. For these diseases, empirical recurrence risks (ie, risks based on direct observation) are estimated by identifying a population of affected individuals and then tabulating the proportion of their relatives who are affected by the same disease. Suppose, for example, that 1000 siblings of individuals affected with a neural tube defect have been identified. If 30 of these siblings are also affected with a neural tube defect, then the empirical recurrence risk is 3%.
Empirical recurrence risks can vary from one population to another because of interpopulation variation in risk factors or can vary temporally, as risk factors change. Thus, empirical risk factors, strictly speaking, are population specific.
Patterns of recurrence risks for multifactorial disorders differ in several important ways from the patterns observed for single-gene disorders:
1. The recurrence risk increases as the number of affected individuals in the family increases. The sibling recurrence risk for a ventricular septal defect, for example, has been estimated at 3% if one sibling is affected. If two siblings are affected in the same family, then the recurrence risk increases to 10%. Recurrence risks for single-gene disorders, in contrast, remain the same regardless of the number of affected individuals in the family. As increasing numbers of individuals affected with a multifactorial disorder are observed in a family, the risk itself does not actually change, but it becomes apparent that the family lies higher on the liability distribution (ie, they have more genetic and/or environmental risk factors), resulting in a higher risk for each sibling.
2. The recurrence risk is higher if the affected individual (the proband) is a member of the less commonly affected sex. As in the pyloric stenosis and autism examples cited above, an affected individual who is a member of the less commonly affected sex is thought to lie higher on the liability distribution. Thus, relatives of this individual have a higher recurrence risk.
Table 171-1. Recurrence Risks for Offspring of Individuals Affected with Pyloric Stenosis
3. The recurrence risk tends to increase if the proband has a more severe expression of the disease. More severe expression of the disease is thought to be correlated with a greater number of liability factors in the family and should produce a higher risk for relatives of the proband. For example, the recurrence risk for relatives of an individual with bilateral cleft lip/palate is higher than that for relatives of an individual with a unilateral cleft.
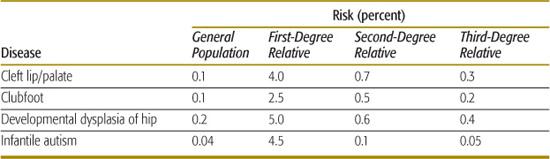
4. The recurrence risk decreases rapidly as the degree of relationship decreases between the proband and his or her relatives. For single-gene disorders, the recurrence risk decreases by one-half for each successive degree of relationship (eg, for an autosomal-dominant disease, the recurrence risk is 50% for siblings, 25% for uncle-niece or grandparent-grandchild relationships, 12.5% for first cousins, and so on). The more rapid decrease seen for multifactorial disorders (see Table 171-2) reflects the fact that many genetic and environmental factors must typically combine to cause the trait, and these are unlikely to be present in less closely related family members.
5. The recurrence risk is correlated with the prevalence of the disease in a population. In single-gene disorders, the recurrence risk is largely independent of prevalence. But for multifactorial disorders, empirical studies have shown that if the population prevalence is p, the sibling risk is approximately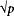 
. The data shown in Table 171-2 indicate that, for many multifactorial diseases, this relationship holds quite well. However, the relationship is only approximate and does not hold for all multifactorial diseases.
TWIN STUDIES: GAUGING THE RELATIVE INFLUENCE OF GENETICS AND ENVIRONMENT
The relative influences of “nature” and “nurture” in human traits have long been a subject of debate. A common method for assessing the relative influence of genetics and environment involves the study of twins, which occur with a frequency of approximately 1 in 100 births in Caucasians (the prevalence is slightly lower in Asians and slightly higher in Africans). Sir Francis Galton, a cousin of Charles Darwin, realized that monozygotic (or identical) twins could be compared with dizygotic (or fraternal twins) to shed light on the nature-nurture question. Monozygotic (MZ) twins, which arise from the early cleavage of the embryo into two virtually identical embryos, share 100% of their genes. Dizygotic (DZ) twins, which are caused by the fertilization of two egg cells by two different sperm cells, are genetically the same as siblings, sharing 50% of their genes. Galton reasoned that a trait strongly influenced by genes should show greater similarity in MZ twins than in DZ twins. For quantitative traits such as height or blood pressure, this similarity is typically measured as an intraclass correlation coefficient, which varies from –1.0 to 1.0. An intraclass correlation of 1.0 indicates a perfect positive association for a trait in all twin pairs, and a correlation of –1.0 indicates a perfect negative association. A correlation coefficient of 0 indicates that there is no association. For present/absent traits, such as neural tube defects, a concordance rate is estimated (ie, if one twin has the trait, how often does the other twin have it?). For traits in which the prevalence varies according to gender, MZ twins are compared with like-sexed DZ twins.
Table 171-2. Prevalence Rates and Recurrence Risks for Several Multifactorial Diseases
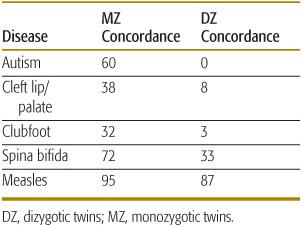
As shown in Table 171-3, traits that are thought to be strongly influenced by genes (such as autism) show substantial differences in similarity in MZ versus DZ twins. Traits unlikely to have a large genetic component, such as measles infection, show little difference in similarity. Concordance rates and correlation coefficients can be used to estimate the heritability of a trait, which is defined as the proportion of variation of a trait that is caused by genetic factors. A common measure of heritability is given by (CMZ – CDZ)/(1 – CDZ), where CMZ is the concordance rate (or correlation coefficient) for a trait in MZ twins and CDZ is the rate in DZ twins. As the difference in CMZ and CDZ increases, heritability goes to 1.0. If there is no difference in the two rates, the heritability is 0.
Although twin studies have been used widely to provide initial estimates of the relative influence of genes on a trait, a number of biases and difficulties confound such studies. Foremost among these is the assumption that the environments of MZ and DZ twins are equally similar. MZ twins are in fact often treated more similarly than are DZ twins, resulting in an environmental bias that tends to increase the MZ concordance rate. This environmental bias has been observed in studies of the heritability of blood pressure, in which heritability estimates based on twin studies are substantially higher than are estimates based on other types of relatives (eg, parents and offspring).
A factor that may work in the opposite direction is the fact that somatic mutations may occur after embryonic cleavage, resulting in MZ twins that are less than 100% genetically identical (clearly, if such a mutation occurs shortly after cleavage, the difference is likely to be greater). Still another factor that can influence the similarity of MZ twins is the uterine environment itself (ie, whether there are separate amnions and chorions, a shared chorion, or shared amnion and shared chorion).
MZ twins who were reared apart are still genetically identical but do not share common environments. Because of the rarity of this situation, few disease conditions have been studied in such twins. However, psychological inventories indicate a remarkable degree of behavioral resemblance in MZ twins reared in separate environments.
Repeated analyses in many different populations have revealed enough consistency to support the use of twin studies to gain an initial impression of the role of genes in disease etiology. Twin studies, of course, do not pinpoint specific genes. Other techniques, such as linkage analysis and positional cloning, must be used to accomplish this goal.
COMMON APPROACHES FOR FINDING GENES UNDERLYING MULTIFACTORIAL DISEASES
Because of the complexity of multifactorial disorders, the identification of individual genes presents a difficult challenge, but several approaches for overcoming this challenge have been developed.
Table 171-3. MZ and DZ Twin Concordance Rates for Selected Pediatric Diseases (percent)
IDENTIFICATION OF HIGHLY HERITABLE SUBSETS
For some multifactorial disorders, subsets of families in which the disease follows mendelian transmission patterns have been identified: autosomal-dominant breast cancer (BRCA1 or BRCA2 mutations) and autosomal-dominant colorectal cancer (APC mutations and mutations in any of the several DNA repair genes that give rise to hereditary nonpolyposis colorectal cancer). Frequently, mendelian subsets of multifactorial diseases are expressed relatively early in life and may have especially severe expression.
In pediatric patients, maturity-onset diabetes in the young (MODY) is often inherited in autosomal-dominant fashion, which provides a useful subset of diabetes cases in which specific causative genes have been identified. About 50% of MODY cases are caused by mutations in the gene that encodes glucokinase, a rate-limiting enzyme involved in the conversion of glucose to glucose-6-phosphate. Mutations of at least 7 other genes are known to cause MODY, and the protein products of these genes are all transcription factors involved in insulin regulation or pancreatic development. The identification of these specific genes and their protein products may lead to a better understanding of the pathophysiology of more common types of diabetes.
Hirschsprung disease (aganglionic megacolon) provides a second example of a childhood disease in which subsets of cases follow a mendelian transmission pattern. In approximately 10% to 20% of Hirschsprung patients, aganglionosis extends beyond the sigmoid colon, and the inheritance pattern is more likely to approximate that of a single-gene disorder. In some families exhibiting autosomal-dominant transmission (with reduced penetrance), loss-of-function mutations in the RET proto-oncogene have been shown to cause the disease. Mutations in the endothelin B receptor gene have been seen in families in which Hirschsprung disease manifests a recessive mode of inheritance.
LINKAGE ANALYSIS
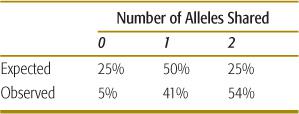
Recurrence risks for multifactorial diseases usually decrease rapidly with more remote degrees of relationship (Table 171-2). Thus, it is difficult to assemble large, extended pedigrees with multiple affected individuals. An alternative is to study only closely related pairs of relatives (most commonly, pairs of siblings both affected with the disorder). To localize genes underlying the trait of interest, DNA polymorphisms located throughout the genome are assayed in each pair of siblings. If a gene underlying the trait lies close to one of the polymorphisms (ie, the polymorphism and the disease gene are linked), then the affected sibling pairs will share a higher proportion of alleles of the polymorphism than would be expected under standard mendelian inheritance. If there is no linkage between a polymorphism and a disease-causing gene, then 25% of siblings will share no alleles of the polymorphism, 50% will share one allele, and 25% will share both alleles. As seen in Table 171-4, a significant proportion of sibling pairs share more alleles than would be expected if there were no linkage between type 1 diabetes and polymorphisms in the class I MHC region. This result provides support for a role of MHC genes in the causation of type 1 diabetes. In a typical sibling-pair linkage analysis, approximately 400 DNA polymorphisms dispersed uniformly throughout the genome are tested (ie, about 1 polymorphism in every 10 million base pairs of DNA).
Table 171-4. MHC Class I Allele Sharing in Siblings Affected with Type I Diabetes
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
