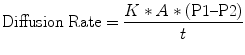In this equation (the alveolar gas equation), P AO2 represents the alveolar partial pressure of oxygen. Additional variables are defined as follows:
The first component needed in the calculation of P AO2 is the P aCO2. This variable can be measured directly from arterial blood. Alternatively, P aCO2 can be approximated from alveolar or expired CO2 in the absence of significant lung disease.
The next element needed to calculate P AO2 is the P IO2. P IO2 is the partial pressure of inspired oxygen and can be calculated using the following formula:
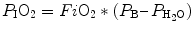
P IO2 incorporates both barometric pressure (P B) and water vapor pressure (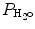
) based on the universal gas law which relates the partial pressures of a combination of gases to their volumes and temperatures. At sea level, P B is 760 mmHg, and P B falls as altitude increases. 
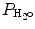must also be considered since inspired gas is warmed and saturated as it moves through the respiratory system. At a normal body temperature of 37 °C, 
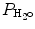is 47 mmHg. Therefore, for inspired room air gas with an FiO2 of 0.21 at sea level, the P IO2 = 0.21 * (760 − 47) = 150 mmHg.
The final component of the alveolar gas equation is the respiratory quotient (R). The respiratory quotient is the ratio of CO2 elimination to O2 consumption, but direct measurement of these two variables is often difficult and impractical in the clinical setting, especially in pediatric and neonatal patients. In most circumstances, R can be estimated to be 0.8, but some variability does exist depending on the dietary balance of carbohydrates, protein, and fat.
Bedside calculation of P AO2 is easily performed using the alveolar gas equation. This calculation provides important clinical data since P AO2 can be used to determine the alveolar-arterial oxygen gradient (P AO2 − P aO2). This difference between oxygenation at the alveolar level versus that measured in arterial blood allows one to assess for adequacy of tissue oxygenation. Normally, a gradient of 5–15 mmHg exists between the partial pressure of oxygen in the alveolus and arterial blood, but this gradient may increase substantially in a number of pathophysiologic states (Table 3.1).
Table 3.1
Causes of hypoxemia
1. Low FiO 2 |
2. Hypoventilation |
3. Ventilation-perfusion mismatch |
4. Impaired alveolar-capillary interface diffusion |
5. Intrapulmonary shunt |
6. Pulmonary artery desaturation |
7. Hemoglobinopathies |
The P AO2 calculation provides an important global measure of alveolar oxygenation, but considerable differences in ventilation exist in different regions of the lung. As one travels from the apex of the lung to the base, ventilation per unit of volume increases (Fig. 3.1). This increase in ventilation is largely related to the effects of gravity, which create higher (or less negative, in the spontaneously breathing patient) intrapleural pressures at the base of the lung relative to the apex. In the supine patient, this difference disappears, and a posterior-anterior gradient is produced with more ventilation per unit of lung volume in the posterior (dependent) portion of the lung. This ventilation gradient, coupled with regional blood flow differences within the lung, has important therapeutic implications and can significantly impact mechanical ventilation strategies for a variety of pathophysiologic states (Radford 1955).
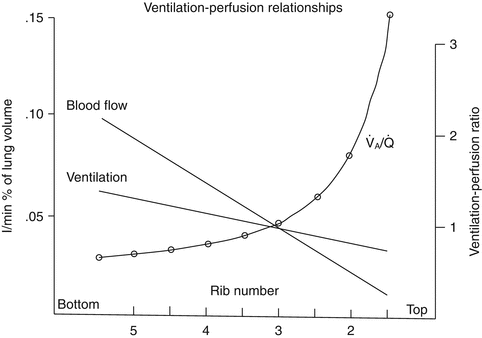
Fig. 3.1
Distribution of ventilation and blood flow and change in ventilation-perfusion ratio down the upright lung (Excerpted from West (2005b))
3.3 Intrapulmonary Shunt
V/Q matching is an important element in pulmonary gas exchange since only the gas that reaches the alveolar-capillary interface is available for exchange. Under ideal circumstances, pulmonary perfusion (Q) would perfectly match the differential ventilation (V) of various lung units and create a ventilation to perfusion ratio (V/Q ratio) of 1. As discussed previously, regional differences exist within the lung, and ventilation is higher in dependent lung units. Similarly, pulmonary perfusion is higher in dependent regions of the lung, but there is a greater change in perfusion across the lung when compared to ventilation. This higher rate of increase in perfusion from nondependent to dependent lung regions leads to imperfect V/Q matching. The different gradients between ventilation and perfusion across the lung lead to a high V/Q ratio (>1) in the nondependent regions and a low V/Q ratio (<1) in the dependent regions (Fig. 3.1). Under normal circumstances, global ventilation is well matched to global perfusion, producing an overall pulmonary V/Q ratio of approximately 0.8.
A small percentage of pulmonary blood flow in the healthy lung travels through non-ventilated portions of the lung, providing an extreme example of V/Q mismatching. This blood represents the intrapulmonary shunt and is sometimes referred to as venous admixture. Some degree of intrapulmonary shunting is normal, and the shunt fraction is defined as the percentage of pulmonary blood flow traveling through non-ventilated lung regions. The normal shunt fraction is less than 5 % and is usually closer to 1–2 % of total pulmonary blood flow (or cardiac output) (Cruz and Metting 1987; West 2005b). Within the normal lung, intrapulmonary shunt is caused by three main factors: (1) desaturated bronchial arterial blood that returns directly to the pulmonary veins after O2 delivery to the bronchi, (2) Thebesian veins which return blood directly to the left ventricle after perfusing the myocardium, and (3) alveolar collapse in the bases or most dependent regions of the lung. These portions of the lung are perfused but unable to be ventilated due to the alveolar collapse, thus, creating a V/Q ratio of 0.
The intrapulmonary shunt fraction can be estimated using the following formula:
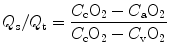where:
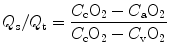
Q s = shunted fraction of cardiac output (intrapulmonary shunt)
Q t = total cardiac output
C cO2 = oxygen content of end pulmonary capillary blood
C aO2 = oxygen content of arterial blood (systemic)
C vO2 = oxygen content of venous blood (pulmonary artery)
Clinically, this formula can provide information regarding the adequacy of gas exchange and the magnitude of intrapulmonary shunt as a potential contributor to inadequate oxygenation. Determining the degree of intrapulmonary shunt may assist in the evaluation of therapeutic options and mechanical ventilation strategies (Cruz and Metting 1987; Fink et al. 2005; Furhman and Zimmerman 2006; Marino 1998). When using this formula clinically to calculate the shunt fraction, a few assumptions are usually involved. When calculating C cO2, the oxygen saturation of hemoglobin (SaO2) is generally assumed to be 100 % due to the fact that in the vast majority of circumstances, blood is fully saturated after traversing the pulmonary capillary. It must be noted that this assumption may not be true in the presence of lung pathology. Furthermore, pulmonary artery catheters are not available in most situations, and mixed venous (SmvO2) or central venous (ScvO2) oxygen saturations can provide a reasonable estimation of hemoglobin saturation in blood returning to the heart for C vO2 calculations. Lastly, all units for oxygen content should be in mL O2/dL blood.
While a small degree of intrapulmonary shunting is normal, there are a number of circumstances in which the shunt fraction may be significantly increased, thus, worsening V/Q mismatch. These pathophysiologic states may lead to regional changes in the lung that impact either pulmonary perfusion, ventilation, or both. This increased intrapulmonary shunt and worsening V/Q mismatch have significant detrimental effects on gas exchange and systemic oxygenation.
Hypoxemia secondary to an intrapulmonary shunt normally does not respond to supplemental oxygen. Increased FiO 2 is ineffective in this circumstance because the shunted blood traveling through capillaries adjacent to non-ventilated lung units is not exposed to the increased alveolar oxygen concentrations. Shunted blood remains desaturated and mixes with fully saturated blood as it returns to the pulmonary veins, causing a less than expected response to oxygen administration (Fig. 3.2).
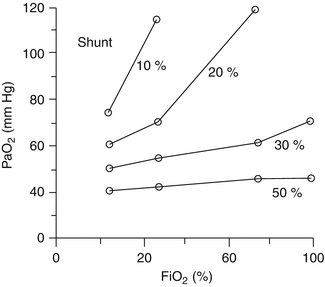
Fig. 3.2
Response to increasing FiO 2 with variation in intrapulmonary shunt fraction (Excerpted from Fink et al. (2005))
Increasing the shunt fraction does not usually influence CO2 elimination. Transient increases in the concentration of CO2 in shunted blood lead to an increased ventilatory drive to increase minute ventilation and maintain a normal P aCO2.
3.4 Dead Space
As previously discussed, a certain quantity of dead space exists in healthy lungs due to the portion of inspired gas that remains in the conducting airways and is unavailable for gas exchange. In direct contrast to intrapulmonary shunting, dead-space ventilation represents “wasted” ventilation to areas of the lung that are poorly perfused, or not perfused at all. In these lung units, the V/Q ratio approaches infinity as perfusion (Q) approaches zero. Anatomic dead space is a fixed volume for a given individual and historically has been estimated as 1 mL/lb (0.45 mL/kg) of body weight (Nunn et al. 1959; Numa and Newth 1996; Furhman and Zimmerman 2006; Fink et al. 2005). Most clinicians feel that this estimate is reasonable, but there are recent data that dispute the accuracy of this approximation (Brewer et al. 2008).
In the absence of lung disease, dead space is composed almost entirely of air that remains in the nasopharynx and conducting airways (anatomic dead space), and there is essentially no alveolar contribution. When lung pathology is present, additional alveolar dead space develops. Alveolar dead space is commonly caused by overdistension of healthy lung units during mechanical ventilation. Other potential causes of alveolar dead space include destruction of the alveolar-capillary membrane, poor cardiac output, and pulmonary vascular obstruction. It should be stressed that alveolar dead space is negligible in the absence of lung disease and anatomic dead space predominates. However, depending on the degree of lung injury, alveolar dead space may be of much greater consequence. Overall, total physiologic dead-space ventilation (anatomic plus alveolar dead space) is described as a ratio to total ventilation and expressed as
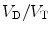where V D is the total volume of dead-space ventilation (including both anatomic and alveolar dead space) and V T is the total inspired volume for a given breath. The V D/V T ratio can be estimated at the bedside using the following modification of the Bohr equation:
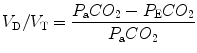where P aCO2 is the arterial partial pressure of CO2 and P ECO2 is the mixed expired concentration of CO2.
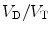
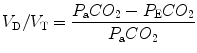
In healthy adults, dead-space ventilation is approximately 20–30 % of total ventilation, yielding a V D/V T of 0.2–0.3. However, pediatric and neonatal patients may have a larger percentage of dead space due to anatomical differences in head and body size, with normal ratios for V D/V T as high as 0.4–0.5 having been reported. In the setting of lung pathology, V D/V T may approach 1, and this change is predominantly due to increases in the degree of alveolar dead space. V D/V T has important therapeutic implications, and clinicians can quickly estimate this ratio at the bedside using easily available data. Not only can the V D/V T ratio be followed as an indicator of the degree of lung injury, but it also may be an important tool in the development of an effective ventilator strategy to optimize V/Q matching.
3.5 Blood-Gas Equilibrium
Adequate matching of ventilation and perfusion depends on diffusion across the interface created at the alveolar-capillary junction. The transfer of both O2 and CO2 is driven by simple diffusion across the alveolar-capillary membrane. As with any gas, this diffusion is governed by Fick’s law (West 2005a, Fink et al. 2005, Furhman and Zimmerman 2006, Marino 1998). The Fick principle states that the rate of gas exchange via passive diffusion depends on properties of both the membrane and the gases involved. Gas transfer rates are directly proportional to the surface area and inversely proportional to the thickness of the membrane. In addition, the solubility coefficient of the gases (which depends on both the intrinsic solubility and the molecular weight of the gas) and the difference between the partial pressures of the gases on opposite sides of the membrane directly contribute to rates of gas transfer. Fick’s relationship between these factors can be represented by the following formula:
