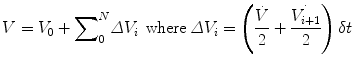and Katherine C. Clement10
(9)
Arkansas Children’s Hospital, 800 Marshall Street, Little Rock, AR 72202, USA
(10)
Department of Pediatrics, Division of Critical Care Medicine, University of North Carolina, CB 7221, Chapel Hill, NC 27517, USA
Educational Aims
To review the physiologic aspects of respiratory mechanics on positive pressure ventilation
To understand the aspects of passive aspects of the respiratory system and its implications on monitoring of respiratory mechanics
To understand the technical aspects of the measurement of respiratory mechanics and potential limitations and applications
Infants and young children have a number of anatomical reasons and physiological reasons for making accurate measurement of respiratory mechanics in the intensive care unit. Despite advances in the measurement of respiratory mechanics in non-intubated infants, these advances have been slow to be adapted to intubated patients due to technical limitations. Thus, the major role of lung function testing in the ICU has been limited to the research arena. However, despite these limitations it is essential the person caring for the intubated pediatric patient have an in-depth understanding of the respiratory mechanics involved with the use of a positive pressure ventilator.
The same model describing the normal interactions between the airways and the lungs can be applied to the interaction of the mechanical ventilator with the respiratory system. In simple terms, the lung-ventilator unit can be considered as a tube with a balloon network at the end, with the tube representing the ventilator tubing, endotracheal tube and airways, and the balloon network of the alveoli. The movement of gas is determined by forces, displacements, and the rate of change of displacements of the components that are distensible.
In physiology, force is measured as pressure (pressure = force/area), displacement is measured as volume (volume = area × displacement), and the relevant rate of change is measured as flow (e.g., average flow = (Δvolume/Δtime); instantaneous flow = dv/dt; the derivative of volume with respect to time). The pressure necessary to cause gas flow into the airways and to increase the volume of gas into the airways and to increase the volume of gas in the lungs is the key component in positive pressure mechanical ventilation. The volume of gas (ΔV) to any lung unit (or balloon in simplified example) and the gas flow  are related to the applied pressure ∆P by
are related to the applied pressure ∆P by
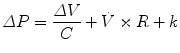 where R is the airway resistance and C is the lung compliance. This equation is known as the equation of motion for the respiratory system. The sum of the muscle pressures and the ventilator pressures is the applied pressure to the respiratory system. Muscle pressure represents the pressure generated by the patients to expand the thoracic cage and lungs. In contrast, ventilator pressure is the transrespiratory pressure generated by the ventilator during inspiration. Combinations of these pressures are generated when a patient is breathing on a positive pressure ventilator. For example, when the respiratory muscles are at complete rest, the muscle pressure is 0; therefore, the ventilator must generate all the pressure necessary to deliver the tidal volume and inspiratory flow. The reverse is also true, and there are degrees of support depending upon the amount of force generated by the patient’s respiratory muscles. Therefore, the total pressure applied to the respiratory system (P RS) of a ventilated patient is the sum of the pressures generated by the ventilator (measured at the airway) P AO and the pressure developed by the respiratory muscles (P MUS). Therefore,
where R is the airway resistance and C is the lung compliance. This equation is known as the equation of motion for the respiratory system. The sum of the muscle pressures and the ventilator pressures is the applied pressure to the respiratory system. Muscle pressure represents the pressure generated by the patients to expand the thoracic cage and lungs. In contrast, ventilator pressure is the transrespiratory pressure generated by the ventilator during inspiration. Combinations of these pressures are generated when a patient is breathing on a positive pressure ventilator. For example, when the respiratory muscles are at complete rest, the muscle pressure is 0; therefore, the ventilator must generate all the pressure necessary to deliver the tidal volume and inspiratory flow. The reverse is also true, and there are degrees of support depending upon the amount of force generated by the patient’s respiratory muscles. Therefore, the total pressure applied to the respiratory system (P RS) of a ventilated patient is the sum of the pressures generated by the ventilator (measured at the airway) P AO and the pressure developed by the respiratory muscles (P MUS). Therefore,
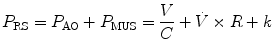 where P RS is the respiratory system pressure, P AO is the airway pressure, and P MUS is the pressure developed by the respiratory muscle.
where P RS is the respiratory system pressure, P AO is the airway pressure, and P MUS is the pressure developed by the respiratory muscle.
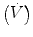 are related to the applied pressure ∆P by
are related to the applied pressure ∆P by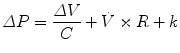
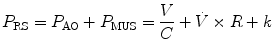
11.2 Terminology and Conventions
Main Symbols:
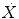
C
Compliance
E
Elastance
f
Frequency
G
Conductance
I
Inertance
PEEP
Positive end-expiratory pressure
P
Pressure
R
Resistance
τ
Time constant (tau)
V
Volume
V T
Tidal volume
Z
Impedance
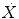
Dot above any symbol indicates first time derivative, e.g., 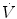 is flow of gas
is flow of gas
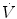 is flow of gas
is flow of gasModifiers:
A
Alveolar
ao
Airway opening
dyn
Dynamic
E
Expiratory
El
Elastic
es
Esophageal
I
Inspiratory
L
Lung
η
Is the viscosity of the gas
p aw
Airway pressure
p l
Pleural
rs
Respiratory system
st
Static
Examples of Combinations
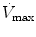
C CW
Chest wall compliance
C dyn
Dynamic compliance
C L
Lung compliance
C st,L
Static lung compliance
E dyn,rs
Dynamic elastance of the respiratory system
P A
Alveolar pressure
P AO
Pressure at airway opening
P bs
Pressure at the body surface (atmospheric pressure)
PEEPi
Intrinsic PEEP
P ES
Esophageal pressure
P plat
Plateau pressure
P pL
Pleural pressure
P RS
Pressure respiratory system
R aw
Airway resistance
R dyn
Dynamic resistance
R ti
Lung tissue resistance
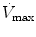
Flow max
11.3 Mechanical Model of the Passive Respiratory System
A model of the respiratory system is considered passive because the lungs respond to forces external to the lungs. The respiratory muscles generate these forces in a patient breathing spontaneously. In contrast, during positive pressure mechanical ventilation, the movement of gases is in response to a pressure gradient that is developed between the airway and the environment. However, in both cases it is the physical impedance of the respiratory system that determines the pattern of response of the lung. Generally the major causes of the impedance can be categorized into either the forces related to the (1) elastic resistance of tissue and alveolar gas/liquid interface and (2) frictional resistance to gas flow. Under static conditions when no gas is flowing, it is the elastic resistance to gas flow that governs the relationship between pressure and lung volume. Minor causes of impedance include the inertia of gas and tissue and the friction of tissue deformation.
It has been recognized that the elastic recoil of the lung is not isolated to the stretching fibers of the lung parenchyma but to the combination of these fibers plus the surface tension acting throughout the vast air/water interface lining the alveoli.
Elastic resistance is only one component of the total impedance to gas flow; a much greater part of the residual forms of impedance are provided by what can be categorized as “nonelastic resistance” provided by resistance to airflow and tissue deformation. These can be categorized as pulmonary resistance and are related to gas flow rate.
In a passive system, the extent of lung inflation reflects a balance between the elastic recoils of the lungs and chest wall, gravitational force, and tension in the respiratory muscles. In this system, when movement occurs, the equilibrium is disturbed and the rate of movement is influenced by the strength of the applied force and by the elasticity, resistance to movement, and the inertia of the thoracic cage, lung tissue, and gas contained in the lung.
Thus, the force applied to a body is met by an opposing force of equal magnitude and is related to the elasticity, resistance, and inertia of the system.
The elasticity of the system can be expressed as elastance which is the reciprocal of compliance (C) and is related to the volume (V), resistance (R), velocity of gas flow, and the inertia (I) to acceleration. All these variables influence the pressure difference across the lung. These can be expressed in Newton’s third law of motion:
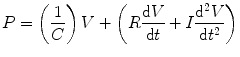
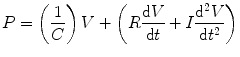
This equation states that a force applied to a body is met by an opposing force of equal magnitude and that this latter force has components related to elasticity, resistance, and inertia.
The necessary force generated to overcome the resistance to movement of the lungs and thorax represents a large energy expenditure and consumption of oxygen. Thus, it is usually the frictional resistance of the lungs and chest wall that limit exercise and the maximal rate that air can move in and out of the lungs. The resistance can be further subdivided into thoracic resistance, pulmonary resistance, lung tissue resistance, and airway resistance.
Inertia according to the laws of physics, force (F) equals mass (M) times acceleration (G = du/dt, where u is the velocity of the gas molecules). Pressure is F/A, where A is the area the force is acting on. The mass of a column of gas is L × A × ρ where L is the length of the column, A its cross-sectional area, and ρ the gas density. From this it follows that
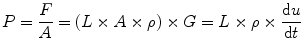
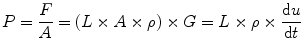
However, u = V/A, and du/dt = (1/A) × dV/dt where V is the volumetric gas flow. dV/dt is the volume acceleration, which is the same as d2 V/dt 2, where V is volume. From this it follows that
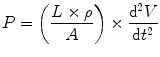
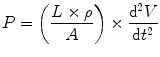
The inertance I therefore equals L × ρ/A. The pressure drop due to inertance is greatest when the flow increases rapidly, as occurs if the frequency of breathing rises. The work performed to achieve the acceleration is stored in the lung as kinetic energy.
Inertial forces are of negligible magnitude except when a high-frequency oscillation is applied for purposes of assisting ventilation or for investigating the mechanical characteristics of the lung.
The forces necessary to overcome the resistance to movement of the lungs and thorax are relatively large and when ventilation is increased requires large energy expenditure and oxygen consumption. Thus, the maximal rate at which air can move into and out of the lungs can be limited. Resistance can be subdivided according to tissue involved including total thoracic resistance, total pulmonary resistance, lung tissue resistance, and airway resistance.
Total thoracic resistance is the sum of the components attributable to the rib cage, the diaphragm, the abdominal wall and contents, the lung tissue, and the gas in the lung and airways. These effects are additive; thus,
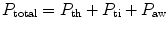 where P is the force required to overcome the frictional resistance and th, ti, aw refer, respectively, to the thoracic rib cage and diaphragm, the lung tissue, and the lung airways. For the thoracic cage the force is a simple function of the velocity of linear movement. The velocity cannot be measured directly but can be described approximately in terms of the rate of airflow. Then, as a first approximation
where P is the force required to overcome the frictional resistance and th, ti, aw refer, respectively, to the thoracic rib cage and diaphragm, the lung tissue, and the lung airways. For the thoracic cage the force is a simple function of the velocity of linear movement. The velocity cannot be measured directly but can be described approximately in terms of the rate of airflow. Then, as a first approximation
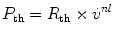 where R th is the resistance of the thoracic cage, in kPa (or cm H2O) l−1s, and
where R th is the resistance of the thoracic cage, in kPa (or cm H2O) l−1s, and 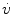 is the airflow (ls− 1). In most instances the value of the exponent n1 lies between 1.0 and 1.1; hence, the relationship is linear.
is the airflow (ls− 1). In most instances the value of the exponent n1 lies between 1.0 and 1.1; hence, the relationship is linear.
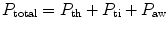
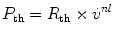
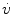 is the airflow (ls− 1). In most instances the value of the exponent n1 lies between 1.0 and 1.1; hence, the relationship is linear.
is the airflow (ls− 1). In most instances the value of the exponent n1 lies between 1.0 and 1.1; hence, the relationship is linear.Total pulmonary resistance is the sum of lung tissue resistance (R ti) and airway resistance (R aw):
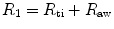 where R 1 is the pulmonary flow resistance in kPa (or cm H2O) l− 1s; it is therefore the pressure difference that must be applied between the pleural surface of the lungs and the lip in order to secure a velocity of flow of 1 l− 1s. This quantity can be derived from the slope of the initial part of the isovolume flow–pressure curve.
where R 1 is the pulmonary flow resistance in kPa (or cm H2O) l− 1s; it is therefore the pressure difference that must be applied between the pleural surface of the lungs and the lip in order to secure a velocity of flow of 1 l− 1s. This quantity can be derived from the slope of the initial part of the isovolume flow–pressure curve.
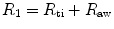
Lung tissue resistance (R ti) normally represents 10 % of the total pulmonary resistance. However, due to changes in airway resistance, its contribution is greater at large as compared to small lung volumes. Tissue resistance can be affected by pathology of the tissue such as in pulmonary fibrosis. It cannot be measured directly; thus, it is estimated by subtracting airway resistance from total pulmonary resistance. This estimation can be inaccurate.
Airway resistance (R ti) is the sum of the resistances attributable to all airways individually. Each airway’s resistance is determined by its diameter that varies with lung volume. Poiseuille’s equation can provide a theoretical basis for understanding resistance of the airway. It states
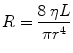 where r is the radius of the tube, L it the length of the tube, and η is viscosity in poise.
where r is the radius of the tube, L it the length of the tube, and η is viscosity in poise.
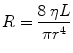
This states that for a simple tube, the resistance is related inversely to the fourth power of the radius (Poiseuille 1840). Because in all airways the radius varies with lung size, the airway resistance varies throughout the respiratory cycle. Thus, resistance is lower at large lung volumes when the airways are expanded; it rises during expiration as the airways diminish in size and becomes infinite at residual volume when some airways close. The reciprocal of airway resistance is conductance (G aw) and increases almost linearly with volume. Specific conductance (sGaw) is G aw/TGV where TGV is thoracic gas volume. It varies less with lung volume than G aw.
In order to overcome the impedance of the respiratory system and to allow gas flow to occur, work must be performed. During breathing, the work overcomes the resistance to movement of the lungs and the chest cage. This work can be categorized by whether the energy is retained or lost from the system. The work performed to overcome the frictional resistance is dissipated as heat and subsequently lost from the system. In contrast, the work performed in overcoming elastic resistance is stored as potential energy and elastic deformation during inspiration and is usually the source of energy for expiration during both spontaneous and artificial breathing. A further discussion of resistance and gas flow will occur in the next section.
11.4 Signals for Respiratory Mechanics Measurements
11.4.1 Measurement Devices (Principles and Technical Requirements)
Our knowledge of physiology is based upon what we are able to measure. In respiratory mechanics for the most part, that is pressure and flow of gas. Modern transducer technology and the availability of computers mean that the pressure and flow can be described and modeled in detail. This is what has led to the preeminent place of mathematical models in respiratory mechanics. However, the success of such models is only as good as the measurements upon which they are based.
The general process by which a biological signal is captured and recorded for analysis is illustrated in Fig. 11.1. A mean feature of this system is the use of a transducer. A transducer is a device that transforms some signal of interest into a signal (usually electrical) that can be recorded.


Fig. 11.1
The general process by which a biological signal is captured and recorded
11.4.1.1 Static Properties
The static properties of a transducer describe its behavior with signals that do not vary with time. In practice one deals with quasistatic signals (almost non-varying with time). However, if the signals were truly static, they would never change and it would be impossible to apply different signals to the transducer. Ideally, one would like to have a transducer that is as linear, stable, and efficient as possible, with the least amount of hysteresis and the greatest signal-to-noise ratio, resolution, and dynamic range.
The signal-to-noise ratio of a transducer is a measure that quantifies how much a signal is corrupted by noise. It is important since a transducer never produces a perfectly accurate representation of a signal. Instead, there is always a bit of unwanted contamination accompanying the measurement.
The resolution of a transducer is the smallest change it can discern in the signal it is measuring. Its dynamic range is the difference between the largest and smallest change in the input that can be accurately measured. The accuracy of a transducer is dependent on its degree of hysteresis and its stability, signal-to-noise ratio, and resolution.
The efficiency of a passive transducer relates to the ratio of the output power over the input power, while powered transducer efficiency depends upon its external power source.
11.4.1.2 Dynamic Properties
The dynamic properties of a transducer describes how its output y(t) is related to its input x(t), when x(t) varies with time (t). If the transducer is nonlinear, then its dynamic response is complex. However, with a stable linear transducer, the properties can be described in terms of its effects on input sinusoids of various frequencies.
Another important property of linear transducers is that they obey the principle of superposition, which means that the output sum of two different waveforms at the input is equal to the sum of the outputs produced by each input individually. Since any input waveform can be expressed as a sum of sinusoids (via the Fourier transform), and each of these sinusoids is altered in an amplitude and phase by an amount that depends only on frequency, the output of a linear transducer can be calculated by figuring out how each component sinusoid of the input is altered and then adding up the results.
11.4.1.3 Frequency Response
The frequency response of a transducer is a description of the way in which it alters sinusoids of different frequencies and consists of two functions A(f) and φ(f). A(f) is the equivalent of the ratio A 1/A 2 above and is called the amplitude response because it is the factor by which a sinusoid of frequency f is altered in amplitude. φ(f) is the equivalent of φ 1 − φ 2 above and is the corresponding alteration in its phase. Transducers can be overdamped or underdamped. The overdamped transducer has an amplitude response A(f) that decreases monotonically with frequency f. When such a transducer is subjected to a sudden steplike change in the input, it responds sluggishly.
An overdamped transducer has an amplitude response A(f) that increases above 1.0 on the step response before eventually falling off with increasing frequency f. When such a transducer is subjected to a sudden steplike change in input, it responds with an overshoot and subsequent “ringing.”
11.4.1.4 Input Impedance
A transducer can never take the role of being a “passive observer.” Whenever a signal is measured by a transducer, the signal itself is always altered to some degree by the transducer itself because energy from the signal is required to produce a change within the transducer. The change in the input signal resulting from the presence of the transducer is inversely related to the transducers input impedance, which obviously should be as high as possible. In particular, the input impedance should be high enough that the change in the measured signal resulting from the presence of the transducer is negligible compared to the resolution of the transducer.
11.4.1.5 Analog-to-Digital Conversion
Data acquisition by a computer requires an analog-to-digital (AD) converter. This is a device that samples the incoming analog voltage signal and converts each voltage reading into a number that can be stored in the computer’s memory. AD converters have resolution depending upon its ability to convert a signal into 4,096–65,536 parts (12 bit to 16 bit converters).
The analog range of an AD converter is the voltage range over which it will accept and digitize a signal. It is desirable to have the voltage signal being sampled fill as much of the analog range of the AD converter as possible, so that the resolution of the digitized signal is maximized. If the voltage signal occupies a small fraction of the analog range, it may suffer discretization error when digitized. A digitized signal that has significant discretization error can be seen to jump about between discrete levels.
11.4.1.6 Transducers for Measuring Pressure and Flow
Today most transducers are solid state. However, traditionally all force transducers consisted of some kind of elastic material whose deformation under the applied force is measured. A piezoresistive force transducer (often called a strain gauge) is one whose resistivity changes as a result of an applied force. An example is a wire whose resistance increases when pulled end to end as it stretches in length and narrows in cross section. The change in resistance of a piezoresistive strain gauge is measured by making the gauge one arm of a Wheatstone bridge (Fig. 11.2). When the bridge is balanced, the output voltage is zero, which occurs when R 1/R 2 = R 3/R 4. As the resistance of R 1 changes, the output voltage V changes from zero. The Wheatstone bridge needs a power supply (a constant DC voltage) and the output voltage usually needs some amplification before being recorded.
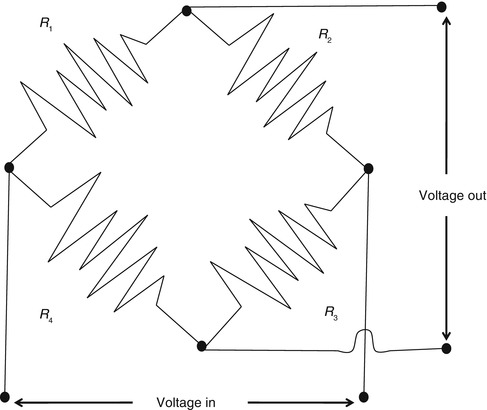

Fig. 11.2
A Wheatstone bridge circuit measuring the change in resistance of a piezoresistive strain gauge
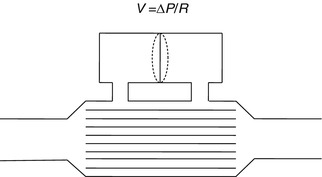
The conventional device used by respiratory physiologists for measuring flow at the tracheal or airway opening is the pneumotachograph which consists of a known resistance (R) across which a pressure difference (ΔP) is measured (Fig. 11.3). The flow 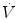 through the device is then calculated as
through the device is then calculated as
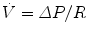
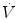 through the device is then calculated as
through the device is then calculated as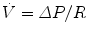

Fig. 11.3
A pneumotachograph, consisting of a differential pressure transducer to measure the drop across a known resistance. R is a known resistance across which a pressure difference is measured. Flow is then calculated by the formula in the diagram
To satisfy the equation above, the known resistance inside the pneumotachograph must be designed so that the flow through it is laminar up to a certain limit. The nature of the flow profile inside the pneumotachograph is affected by the shape of the conduit leading into it, so it is advisable to have straight lengths of tubing leading into the pneumotachograph in both directions. This conditions the flow before it reaches the point where ΔP is measured. Some pneumotachographs also contain heating elements or shells so that moisture will not condense in the resistor and change its characteristics during use.
A problem with the pneumotachograph is the frequency response of a pneumotachograph can be rather limited. If a rapidly responding pressure transducer is used with the shortest possible connection between the transducer ports and those of the pneumotachograph, the frequency response of a typical pneumotachograph may be relatively flat up to 20 Hz or so. Eventually the device achieves a resonance. It is important to keep the tubing on the pneumotachograph as short as possible.
Another aspect of the pneumotachograph that can cause problems is its input impedance. If the flow of gas required to travel between the pneumotachograph and the differential pressure transducer (in order to pressurize the latter) is significant compared to the flow through the pneumotachograph itself, then there can be significant differences between the flow through the device and the differential pressure recorded. This problem becomes worse as the diameter of the pneumotachograph decreases with the tubing and pressure transducer remaining the same. It also becomes worse as the frequency of the flow through the device increases because it may take some time for the differential pressure transducer to become pressurized via the lateral ports, resulting in phase differences between the recorded differential pressure and the flow. However, some of these limitations due to size can be overcome by utilizing a technique such as force oscillation (Schuessler and Bates 1995).
11.4.2 Airway Gas Flow
The resistance to airflow in a tube depends on the type of flow, the dimensions of the tube, and the viscosity and density of the gas. Airflows through tubes can either be laminar or turbulent.
11.4.2.1 Laminar Flow
Laminar flow can be described as organized, and the streamlines are everywhere parallel to the sides of the tube and are capable of sliding over one another. The streamlines at the center of the tube move faster than those close to the walls, producing a flow profile that is parabolic. With laminar flow, the relation between pressure and flow is given by Poiseuille’s equation:
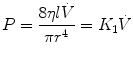 or
or
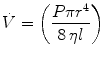 where
where 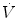 is the flow rate; P is the driving pressure (pressure drop between the beginning and the end of the tube); r and l are the radius and the length of the tube, respectively; and η is the viscosity of the gas. Because flow resistance (R) is the driving pressure divided by the flow, the resistance with laminar flow is independent of the flow rate:
is the flow rate; P is the driving pressure (pressure drop between the beginning and the end of the tube); r and l are the radius and the length of the tube, respectively; and η is the viscosity of the gas. Because flow resistance (R) is the driving pressure divided by the flow, the resistance with laminar flow is independent of the flow rate:
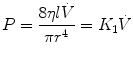
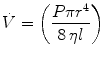
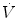 is the flow rate; P is the driving pressure (pressure drop between the beginning and the end of the tube); r and l are the radius and the length of the tube, respectively; and η is the viscosity of the gas. Because flow resistance (R) is the driving pressure divided by the flow, the resistance with laminar flow is independent of the flow rate:
is the flow rate; P is the driving pressure (pressure drop between the beginning and the end of the tube); r and l are the radius and the length of the tube, respectively; and η is the viscosity of the gas. Because flow resistance (R) is the driving pressure divided by the flow, the resistance with laminar flow is independent of the flow rate:Laminar flow 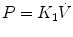
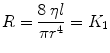
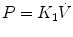
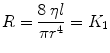
Note the critical importance of the tube radius. If the radius of the tube is halved, the airway resistance increases 16-fold. Note also that laminar flow is dependent on the viscosity of gas but is independent of its density.
11.4.2.2 Turbulent Flow
Turbulent flow occurs at high flow rates and is characterized by a complete disorganization of the streamlines so that molecules of gas move laterally, collide with one another, and change velocities. Owing to this disorganization, the pressure drop across the tube is not proportionate to the flow rate as with laminar flow but rather is proportional to the square of the flow rate:
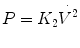
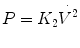
Thus, the resistance to airflow is proportional to the flow rate:
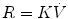 in contrast with laminar flow. In addition, with turbulent flow, there is an increase in the pressure drop for a given flow, but the viscosity of the gas becomes unimportant.
in contrast with laminar flow. In addition, with turbulent flow, there is an increase in the pressure drop for a given flow, but the viscosity of the gas becomes unimportant.
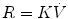
11.4.2.3 Reynolds Number
Whether the airflow is laminar or turbulent depends to a large extent on a dimensionless quantity called the Reynolds number, Re, which is given by
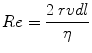 where r is the radius of the tube, v is the average velocity, d is the density of the gas, and η is the viscosity of the gas. In a straight, smooth, rigid tube, turbulence occurs when Re exceeds 2,000.
where r is the radius of the tube, v is the average velocity, d is the density of the gas, and η is the viscosity of the gas. In a straight, smooth, rigid tube, turbulence occurs when Re exceeds 2,000.
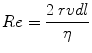
In the lung, laminar flow occurs only in small peripheral airways, where, owing to the large overall cross-sectional area, flow through any given airway is extremely slow. Turbulent flow occurs in the trachea. In the remainder of the lung, owing in large part to the multiple branching of the tracheobronchial tree, flow is neither laminar nor turbulent but rather mixed or transitional. With transitional flow pattern, flow is dependent on both the viscosity and the density of the gas:
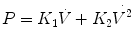
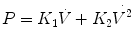
11.4.2.3.1 Threshold Resistors
A threshold resistor is a resistor that allows no gas to pass until a threshold pressure is reached. Once that pressure is reached, gas passes freely with little further rise in pressure as the flow rate increases. The Starling valve (Fig. 11.4) is the classic prototype of the threshold resistor. In this model gas will only flow when the upstream pressure exceeds the pressure in the chamber surrounding the collapsing tubing. Another example of a threshold resistor is a spring-loaded valve that was commonly used in ventilators to maintain end-expiratory pressure.
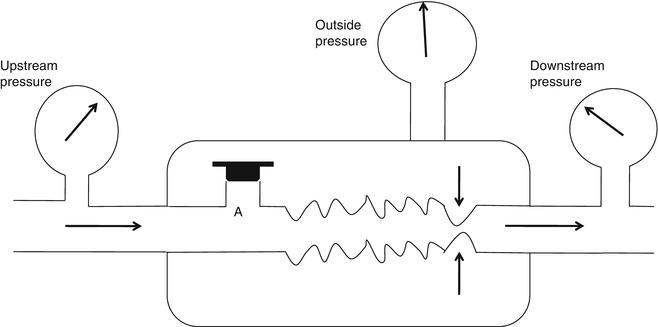

Fig. 11.4
The Starling resistor consists of a length of a flaccid collapsible tubing passing through a rigid box. When the outside pressure surrounding the tube exceeds the upstream pressure, the tubing collapses as illustrated by the arrows. Thus, no gas can flow no matter the level of downstream pressure. If orifice A is opened, the outside pressure rises with the upstream pressure and so limits flow rate to a level which is independent of the magnitude of the upstream pressure
Another property of the threshold resistor is that once gas begins to flow, an increase in downstream pressure will distend the tubing thus decreasing the resistance of the device. However, a decreased downstream pressure cannot initiate flow. This model can also be used to explain the behavior of a collapsing airway during expiration.
11.4.3 Airway Pressure
The airway pressure is the force that the mechanical ventilator and patient apply on the respiratory system. The measurement requires of a pressure transducer. Pressure transducers used in clinical practice are essentially of two types: (1) variable reluctance transducer, where an element is deformed by the pressure changing the magnetic flux linkage between two coils receiving electrical current, and (2) piezoresistive transducers where there is an element that when deformed changes the resistance to electrical current.
The airway pressure (P aw) may be measured at different points of the mechanical ventilator–patient circuit. A pressure sensor or transducer may be placed at the airway opening, P AO (the Y-piece just before connecting to the endotracheal tube); at the inspiratory or expiratory ventilator outlets; or at the trachea (using a catheter). The place of measurement of airway pressure may yield different results, as the effects of the interface (circuit, humidifier, and endotracheal tube) may interfere with the measurements. Almost all current mechanical ventilators have sensors for airway pressure; if absent, P aw can be measured with stand-alone devices.
The effect of flow in the accuracy of airway pressure measurements must be accounted. During dynamic conditions, there is flow as a result of a driving pressure. The effect of flow and the position of the pressure transducer are described by the Bernoulli effect. If a catheter or an opening in the system, where the pressure is going to be measured, is perpendicular to the direction of flow, the value measured is the lateral pressure (P lat) rather than the driving pressure. The following equation demonstrates the factors that affect the P lat. The P lat is lower than the driving pressure, unless there is no flow (P stat), or if the cross-sectional area where the pressure being measured is large.
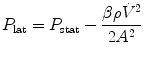 where P stat is the static pressure, A is cross-sectional area,
where P stat is the static pressure, A is cross-sectional area, 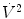 is flow, ρ is density of the gas, and β is the flow velocity profile (1 = linear, 2 = parabolic).
is flow, ρ is density of the gas, and β is the flow velocity profile (1 = linear, 2 = parabolic).
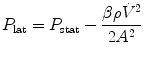
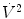 is flow, ρ is density of the gas, and β is the flow velocity profile (1 = linear, 2 = parabolic).
is flow, ρ is density of the gas, and β is the flow velocity profile (1 = linear, 2 = parabolic).The Bernoulli effect can be eliminated by the use of an opening or catheter for measurement that faces the flow; this is called a pitot tube. By facing the flow, the opening of the tube makes a small amount of gas to stop, and hence, the effect of flow is eliminated and we can measure P stat.
The P aw is the transrespiratory system pressure and is a manifestation of the respiratory system characteristics (elastic P EL and resistive P R):
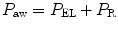
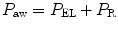
This can be written as
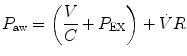 where V indicates volume relative to the end-expiratory position, C is compliance, P ex is end-expiratory alveolar pressure,
where V indicates volume relative to the end-expiratory position, C is compliance, P ex is end-expiratory alveolar pressure, 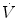 is flow, and R is resistance.
is flow, and R is resistance.
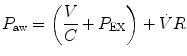
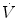 is flow, and R is resistance.
is flow, and R is resistance.During static conditions, the airway pressure is a manifestation of the respiratory system compliance:
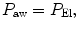 or
or
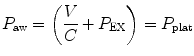
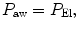
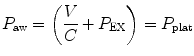
During mechanical ventilation, the airway pressure signal (Fig. 11.5) may be used to obtain direct measurements (peak inspiratory pressure, plateau pressure) or calculated parameters (mean airway pressure).
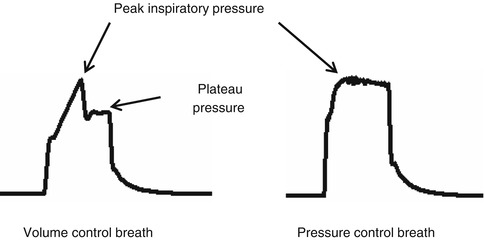

Fig. 11.5
Airway pressure signal according to mode of ventilation
The peak inspiratory pressure (PIP) is the maximum pressure during assisted ventilation. According to the mode of ventilation, the value may represent different respiratory system characteristics. In a volume- or flow-controlled mode, the PIP is the manifestation of the respiratory system compliance, resistance, and patient effort (Fig. 11.6). In a pressure-controlled mode, the PIP is a manifestation of the operator set inspiratory pressure.
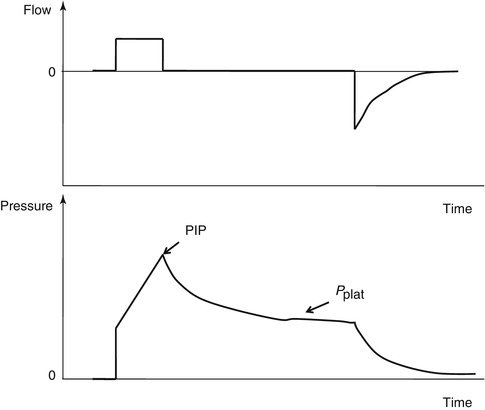

Fig. 11.6
The figure shows flow–time and pressure–time waveforms from a constant flow mode of ventilation and illustrates various landmarks for the waveform
The plateau pressure, P plat, is the airway pressure during an inspiratory hold while a patient is on mechanical ventilation. By creating an inspiratory hold, the effects of lung resistance and impedance are annulled, leaving a measure of the respiratory system compliance. As described before, the respiratory system compliance is a manifestation of the lung, chest wall, and abdomen.
The mean airway pressure, 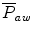 , is the average pressure of the airway over a given time interval. In a static model, where all the breaths are identical, the mean airway pressure is the area under the curve of a pressure–time curve for one breath divided by the total cycle time (inspiration + exhalation). In an active model, the mean airway pressure can be calculated as an average over several breaths. Several mechanical ventilators will display a
, is the average pressure of the airway over a given time interval. In a static model, where all the breaths are identical, the mean airway pressure is the area under the curve of a pressure–time curve for one breath divided by the total cycle time (inspiration + exhalation). In an active model, the mean airway pressure can be calculated as an average over several breaths. Several mechanical ventilators will display a 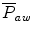 value; it depends on the brand of mechanical ventilator and the technique it uses to measure it. Some use a number of breaths, while others do it breath to breath. To obtain the measurement, the ventilator or measuring instrument must average a large number of pressure measurements.
value; it depends on the brand of mechanical ventilator and the technique it uses to measure it. Some use a number of breaths, while others do it breath to breath. To obtain the measurement, the ventilator or measuring instrument must average a large number of pressure measurements.
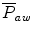 , is the average pressure of the airway over a given time interval. In a static model, where all the breaths are identical, the mean airway pressure is the area under the curve of a pressure–time curve for one breath divided by the total cycle time (inspiration + exhalation). In an active model, the mean airway pressure can be calculated as an average over several breaths. Several mechanical ventilators will display a
, is the average pressure of the airway over a given time interval. In a static model, where all the breaths are identical, the mean airway pressure is the area under the curve of a pressure–time curve for one breath divided by the total cycle time (inspiration + exhalation). In an active model, the mean airway pressure can be calculated as an average over several breaths. Several mechanical ventilators will display a 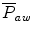 value; it depends on the brand of mechanical ventilator and the technique it uses to measure it. Some use a number of breaths, while others do it breath to breath. To obtain the measurement, the ventilator or measuring instrument must average a large number of pressure measurements.
value; it depends on the brand of mechanical ventilator and the technique it uses to measure it. Some use a number of breaths, while others do it breath to breath. To obtain the measurement, the ventilator or measuring instrument must average a large number of pressure measurements.The formula to calculate P aw is
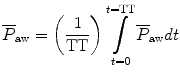 where TT is the total cycle time in seconds.
where TT is the total cycle time in seconds.
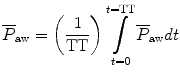
The 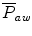 will be affected by the PIP, PEEP, type of pressure waveform, frequency, and inspiratory and expiratory time. The larger the PIP, PEEP, frequency, and inspiratory time, the higher the
will be affected by the PIP, PEEP, type of pressure waveform, frequency, and inspiratory and expiratory time. The larger the PIP, PEEP, frequency, and inspiratory time, the higher the 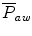 . The larger the PEEP, the lower the
. The larger the PEEP, the lower the 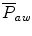 . The closer the waveform is to a perfect square, the higher the
. The closer the waveform is to a perfect square, the higher the 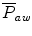 . At a single-compartment level with linear equal inspiratory and expiratory resistance,
. At a single-compartment level with linear equal inspiratory and expiratory resistance, 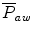 is equal to the mean alveolar pressure. If the inspiratory resistance is higher than the expiratory resistance, the
is equal to the mean alveolar pressure. If the inspiratory resistance is higher than the expiratory resistance, the 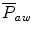 will be higher than the mean alveolar pressure. If the expiratory resistance is higher than the inspiratory resistance, the
will be higher than the mean alveolar pressure. If the expiratory resistance is higher than the inspiratory resistance, the 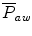 will be lower than the alveolar pressure.
will be lower than the alveolar pressure.
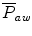 will be affected by the PIP, PEEP, type of pressure waveform, frequency, and inspiratory and expiratory time. The larger the PIP, PEEP, frequency, and inspiratory time, the higher the
will be affected by the PIP, PEEP, type of pressure waveform, frequency, and inspiratory and expiratory time. The larger the PIP, PEEP, frequency, and inspiratory time, the higher the 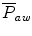 . The larger the PEEP, the lower the
. The larger the PEEP, the lower the 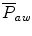 . The closer the waveform is to a perfect square, the higher the
. The closer the waveform is to a perfect square, the higher the 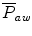 . At a single-compartment level with linear equal inspiratory and expiratory resistance,
. At a single-compartment level with linear equal inspiratory and expiratory resistance, 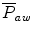 is equal to the mean alveolar pressure. If the inspiratory resistance is higher than the expiratory resistance, the
is equal to the mean alveolar pressure. If the inspiratory resistance is higher than the expiratory resistance, the 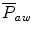 will be higher than the mean alveolar pressure. If the expiratory resistance is higher than the inspiratory resistance, the
will be higher than the mean alveolar pressure. If the expiratory resistance is higher than the inspiratory resistance, the 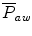 will be lower than the alveolar pressure.
will be lower than the alveolar pressure.11.4.4 Transesophageal Pressure (Meaning and Measurement)
The esophagus lays in the posterior mediastinum inside the thorax and is surrounded by a scant amount of soft tissue and the pleura. Its location allows to use transducers to obtain pressure measurements (Fig. 11.7). The changes in esophageal pressure, ΔP es, correlates and is used as a surrogate for the changes in intrapleural pressure, ΔP pl. The position of the patient (supine versus prone or standing), type of catheter used, and underlying condition may affect pleural pressures (Washko et al. 2006). Nonetheless, P ES as a surrogate of P pl allows the practitioner to obtain and calculate and separate the lung and chest wall compliances from the respiratory system compliance. As follows,
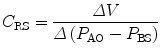 where ΔV is change in volume, P AO is the pressure at the airway opening, and P BS is pressure at the body surface. During mechanical ventilation, this value is ΔV = V t, and Δ(P aw − P BS) is (P plat − PEEPTOT) (in the setting of mechanical ventilation, P BS can be substituted by total PEEP). If we take into consideration the P ES as a marker of P pl, then we can divide the respiratory system compliance into lung and chest wall:
where ΔV is change in volume, P AO is the pressure at the airway opening, and P BS is pressure at the body surface. During mechanical ventilation, this value is ΔV = V t, and Δ(P aw − P BS) is (P plat − PEEPTOT) (in the setting of mechanical ventilation, P BS can be substituted by total PEEP). If we take into consideration the P ES as a marker of P pl, then we can divide the respiratory system compliance into lung and chest wall:
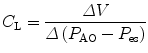
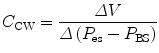
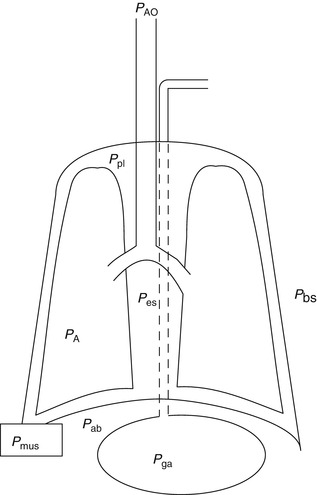
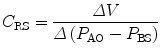
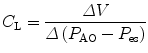
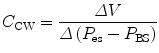

Fig. 11.7
Diagram of the respiratory system: P AO pressure at the airway opening, P pl pleural pressure, P es esophageal pressure, P bs body surface pressure, P A alveolar pressure, P mus muscle pressure, P ab abdominal pressure, P ga gastric pressure
The measurement of the esophageal pressure can be done with a balloon-tipped catheter, a liquid-filled catheter, or a transducer at the tip of a catheter. The most common method is the balloon-tipped catheter.
The placement of an esophageal balloon is essential to obtain consistent measurements. The catheter is inserted under topical lubrication and in some cases topical anesthesia through the nose. The catheter is advanced to the gastric chamber, where, if the patient is actively breathing, the balloon will demonstrate positive deflections (the abdominal pressure increases during inspiration). The esophageal catheter is then retrieved until negative deflections are seen; from that point one must retract the esophageal balloon the amount of distance to maintain the whole balloon in the thoracic esophagus. It is essential to use low volumes to inflate the balloon (<1 cc air) as this will cause false elevation in the measurements.
To ensure that the balloon catheter is appropriately placed, the patient or clinician must generate transpulmonary pressure swings so that the ΔP es and ΔP AO can be compared. In a patient who can cooperate, the maneuver consists of measuring the P AO and P ES simultaneously while the patient performs forceful breathing efforts. The most common test used to assess accuracy is the dynamic “occlusion test.” It is performed by occluding (blocking) the airway while 3–5 respiratory efforts happen. The ΔP es and ΔP AO are then compared. A ratio of difference between ΔP es/ΔP AO should approach 1 to ensure measurement agreement.
11.4.4.1 Alveolar Pressure
Direct measurement of alveolar pressure in patients is not feasible but has been performed in animal studies. Subpleural alveolar pressure (P A) is measured using an alveolar capsule technique. A small plastic capsule is attached to the exposed pleural surface and a small area is punctured with a needle and isolated so changes can be measured utilizing a small piezoresistive pressure transducer. Multiple sites can be measured simultaneously.
11.5 Measurement of Passive Respiratory Mechanics
11.5.1 Mechanics of the Passive Respiratory System
The two most common methods of measuring passive mechanics are the single and multiple occlusion techniques. For the occlusion technique, the Hering–Breuer reflex must be invoked to elicit relaxation of the respiratory system, thus allowing accurate assessment of respiratory mechanics measurements. To perform these techniques, airflow, pressure, and volume changes at the mouth must be recorded and analyzed.
As stated previously a model of the respiratory system is considered passive because the lungs respond to forces external to the lungs. The single-compartment linear model is linear because its independent variables  are linearly related to the dependent variable P.
are linearly related to the dependent variable P.
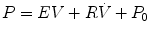
 are linearly related to the dependent variable P.
are linearly related to the dependent variable P.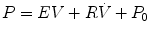
The single-compartment linear model can be made more realistic by adding extra features in two ways: (1) by making it nonlinear and (2) by adding more mechanical degrees of freedom.
The resistive pressure drop can be made nonlinear as follows, which includes two resistive parameters and flow squared:
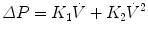
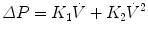
This equation is used to describe a conduit with both laminar and turbulent fluid flow known as the Rohrer’s equation.
Further, the elastic pressure nonlinear can be converted as follows:
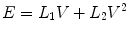
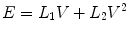
11.5.2 Resistance, Compliance, Inertance, Tissue Damping, and Elastance
11.5.2.1 Resistance
Resistance during mechanical ventilation describes the airflow conditions during both inspiration and expiration. Resistance represents the flow-resistive elements of the respiratory system. It is expressed as a pressure variation over gas flow using the following general equation:
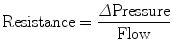
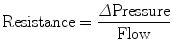
By substituting standard units, it becomes
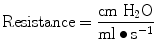
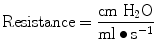
Flow, tidal volume, and the dimensions of the ventilator and airway components affect airway resistance. The size of the endotracheal tube is an important element in gas flow through the breathing circuit and thus affects the measured resistance. When delivering a set tidal volume, the volume at a set flow is affected by a smaller and longer tube that will produce larger resistance to gas flow.
11.5.2.1.1 Compliance and Elastance
Compliance is how much a compartment will expand if the pressure in that compartment is changed. A balloon has a high compliance because a small pressure increase inside the balloon will greatly expand the balloon. A rigid tube has a low compliance because a small pressure increase inside the rigid tube will not result in a significant increase in the volume of the rigid tube. Two major forces contribute to lung compliance: tissue elastic forces and surface tension forces. The compliance (C) is determined by the change in elastic recoil pressure (ΔP) produced by a change in volume (ΔV):
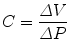
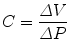
The compliance of the lungs (C L), chest wall (C CW), and respiratory system (C RS) can be determined by measuring the change in distending pressure and the associated change in volume. The distending pressure represents the pressure change across the structure. Where P ao, P pl, and P bs represent the pressure measured at the airway opening, pleural pressure, and pressure at the body surface (atmospheric pressure), respectively.
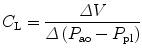
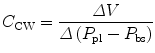
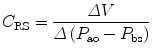
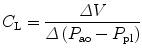
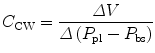
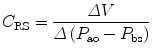
Lung volume and volume–pressure relationships (e.g., compliance) reflect parenchymal (air space) development, whereas airflow and pressure–flow relationships (resistance and conductance) predominantly reflect airway development. The lungs become stiffer (compliance decreases) at higher lung volumes.
Total respiratory compliance (C rs) is related to lung compliance and chest wall compliance by the following equation:
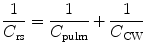
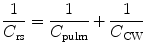
Total static compliance (during no flow activity at the end of inspiration and expiration) and total dynamic characteristics (during active inspiration) are usually monitored via a volume–pressure relationship during mechanical ventilation.
11.5.2.2 Chest Wall Compliance
Chest wall compliance (C CW) describes the changes in tidal volume (V T) relative to the pleural pressure, reflected by the esophageal pressure (P eso), and is expressed by the following equation:
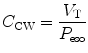
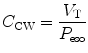
To calculate chest wall compliance, the patient should be completely passive. In patients this is usually accomplished by the use of a neuromuscular blocking agent or inducing apnea by hyperventilation, thus removing respiratory drive. Chest wall compliance is an essential component in the calculation of total work of breathing.
11.5.2.3 Lung Compliance
Lung compliance (C pulm) describes the changes in tidal volume relative to transpulmonary pressure P plat − P eso where P plat is the plateau pressure, also referred to as the alveolar pressure, and P eso is the esophageal pressure under quasistatic conditions.
Lung compliance is expressed by the following equation:
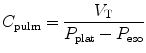
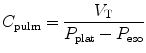
Lung compliance can be obtained on passively or spontaneously breathing patients.
11.5.2.4 Elastance
Elastance is defined as the change in distending pressure divided by the associated change in volume:
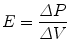
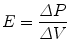
Elastance is therefore the reciprocal of compliance; thus, stiff lungs have a high elastance. The end-inspiratory airway occlusion method is clinically used to measure the static compliance of the respiratory system or its reciprocal, elastance of the respiratory system (E st, rs), according to the following equation (Rossi et al. 1998):
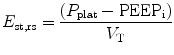 where P plat is plateau pressure obtained after occlusion of the airway, PEEPi is intrinsic positive end-expiratory pressure (PEEP), and V T is tidal volume.
where P plat is plateau pressure obtained after occlusion of the airway, PEEPi is intrinsic positive end-expiratory pressure (PEEP), and V T is tidal volume.
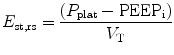
11.5.2.5 Inertance
Inertance of the respiratory system is the analog of inertia and is a measure of the tendency of the respiratory system to resist changes in flow. Forces due to inertance increase with increasing frequency, and since they are opposite in direction to those forces produced by elastance, resistance is thus reduced. At normal respiratory frequencies, inertance is usually insignificant. The inertance I therefore equals L × ρ/A. The pressure drop due to inertance is greatest when the flow increases rapidly, as occurs if the frequency of breathing rises.
11.5.2.6 Tissue Damping
Tissue damping is closely related to tissue resistance and reflects the energy dissipation in the lung tissues. Tissue damping is independent of frequency. In a constant phase model, the calculation of input impedance is
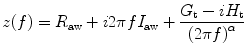 where
where
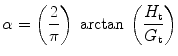 R aw represents the resistance of the pulmonary airways to gas flow, I aw is the inertance of the gas in the airways, G t (tissue damping) characterizes viscous dissipation of energy within the lung tissues during inflation and deflation, and H t (tissue elastance) characterizes energy storage in the tissues. G t is thus related to tissue resistance, while H t is related to tissue elastance.
R aw represents the resistance of the pulmonary airways to gas flow, I aw is the inertance of the gas in the airways, G t (tissue damping) characterizes viscous dissipation of energy within the lung tissues during inflation and deflation, and H t (tissue elastance) characterizes energy storage in the tissues. G t is thus related to tissue resistance, while H t is related to tissue elastance.
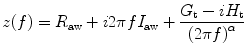
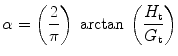
11.5.3 Dynamic Hyperinflation
When breathing on the ventilator with increased time constants secondary to increased inspiratory resistance, hyperinflation develops secondary to incomplete emptying of the lung during expiration. For the patient to generate inspiratory airflow in the next breath, the patient must generate a negative pressure equal in magnitude to the opposing elastic recoil pressures. Secondary to these increased elastic load related to the patient, there is a shift in their compliance curve to the upper less compliant part of the curve. This coupled with a decrease in the efficiency of force generation by their respiratory muscles increases their work of breathing. In a patient breathing on the ventilator, this elevated static recoil pressure leads to intrinsic PEEP or static PEEPi. PEEPi poses a significant inspiratory threshold that has to be fully counterbalanced by increasing inspiratory muscle effort in order to generate a negative pressure in the central airways in order to trigger the ventilator.
11.5.4 Principals and Practice of Classical Measurement of Respiratory System
Most techniques for measuring the mechanics of the respiratory system are based on the assumption that a single balloon on a pipe can model the lung. When breathing is simulated in this model, the balloon is inflated and deflated and the dynamics of the system may be described by the general equation of motion for a linear single-compartment model (SCM):
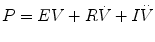
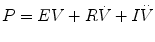
That is, the driving pressure of the system (P) is the sum of its elastic (EV = elastance × volume), resistance 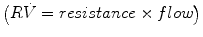 , and inertive
, and inertive 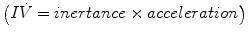 components. For the most practical applications, the contribution of inertance in this equation is negligible and can be ignored. Thus, the equation can be written as follows:
components. For the most practical applications, the contribution of inertance in this equation is negligible and can be ignored. Thus, the equation can be written as follows:
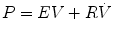
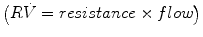 , and inertive
, and inertive 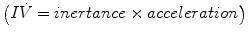 components. For the most practical applications, the contribution of inertance in this equation is negligible and can be ignored. Thus, the equation can be written as follows:
components. For the most practical applications, the contribution of inertance in this equation is negligible and can be ignored. Thus, the equation can be written as follows: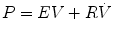
If we apply this equation to the respiratory system during mechanical ventilation, dynamic elastance (E RS) (or compliance (C RS)) and dynamic resistance (R RS) may be estimated by relating pressure measured at the airway opening (P ao) to simultaneous measurements of flow 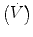 and volume (V).
and volume (V).
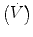 and volume (V).
and volume (V).The equation of motion for an SCM of the respiratory system is as follows:
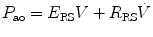
or
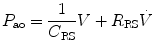
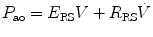
(11.11)
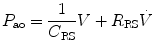
Similarly, dynamic lung elastance (E l) and lung resistance (R l) may be calculated by relating transpulmonary pressure (P tp) to flow and volume. The P tp may be calculated by subtracting pleural pressure estimate form and esophageal catheter (P es) from airway opening pressure measurements (P tp = P ao − P es). The equation of motion for an SCM of the lung is
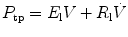
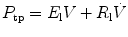
11.5.5 Simplified Methods to the Measurement of Total Respiratory Mechanics
There are a number of published articles describing different techniques to measure dynamic respiratory mechanics in children. Below is a summary of some of those techniques.
11.5.5.1 Mead–Whittenberger Technique
Traditionally this technique has been used to measure dynamic compliance (C dyn) and resistance (R dyn) in spontaneously breathing subjects (Mead and Whittenberger 1953). This technique assumes that resistance and compliance are constant throughout inspiration and expiration. Changes in transpulmonary pressure (P tp) are related to changes in flow and volume over the tidal volume range. Compliance is calculated by examining the points of zero flow at end-inspiration and end-expiration. The pressure change and corresponding volume change between these points can be used to determine dynamic compliance, 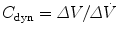 , and is measured during expiration. Similarly, dynamic resistance is measured as a change in flow between points of equal volume in the mid-volume range
, and is measured during expiration. Similarly, dynamic resistance is measured as a change in flow between points of equal volume in the mid-volume range 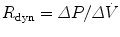 . Under these conditions elastic forces are assumed to be equal and opposite.
. Under these conditions elastic forces are assumed to be equal and opposite.
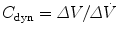 , and is measured during expiration. Similarly, dynamic resistance is measured as a change in flow between points of equal volume in the mid-volume range
, and is measured during expiration. Similarly, dynamic resistance is measured as a change in flow between points of equal volume in the mid-volume range 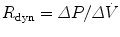 . Under these conditions elastic forces are assumed to be equal and opposite.
. Under these conditions elastic forces are assumed to be equal and opposite.A limitation of this technique is that the assumption of equality of resistance and compliance throughout both inspiration and expiration may not be true for measurements with evidence of hyperinflation. This may be difficult to apply to ventilated subjects as the points when flow = 0 at mid-tidal and end-tidal volume occur with rapidly changing pressure patterns. Some of these limitations may be overcome utilizing the technique of handbagging the patient during the measurement.
11.5.5.2 Mortola–Saetta Method
This is a method which is a variation of the least-squares regression technique described below. This technique involves occluding the airways of spontaneously breathing subject at end-expiration with a resultant inspiratory effort against the occlusion. This effort results in a pressure change, which is thought to reflect the driving pressure of the respiratory system. When pressure is measured at known intervals from the beginning of inspiration, it can be by the measurement of volume from the corresponding time points during the previous unoccluded breaths and plotted against the flow/volume relationship. In this model, the slope of this relationship is a measure of lung resistance and the intercept is a measure of lung elastance (Mortola and Saetta 1987).
11.5.5.3 Volume Corrected Resistance
As can be inferred by the name, this technique corrects the measurement of resistance from the pressure–flow relationship for changes over the tidal volume range. By plotting pressure divided by flow (R dyn) against volume, resistance can be examined over the tidal volume range (Beardsmore et al. 1986).
11.5.5.4 Forced Oscillation Technique
Forced oscillation technique is a general term for methods that apply broadband flow signals to the airway opening, with a measure of the resulting pressure also at the airway opening or at the body surface (Solymar et al. 1989). This technique allows the calculation of respiratory impedance that includes both the resistive and elastic properties of the system. This technique requires a signal-producing device that is usually either done with a loud speaker or a piston oscillator.
The key measurement considerations when implementing the forced oscillation techniques relate to characteristics of the flow transducer, filtering, error reduction, and sampling. For this technique pressure and flow transducers must be linear over the range of interest. The frequency response of pressure and flow transducers must be adequate over the frequency range investigated. Most importantly, they must be matched. The dynamic common mode rejection ratio of the flow transducer must be high over the frequency range of interest (i.e., input impedance must be high). Appropriate filtering for anti-aliasing must be done, so as to satisfy the sampling theorem. In order to minimize discretization error, the pressure and flow signals must be suitably amplified to occupy a significant fraction of the A/D converter range. Data must be sampled at greater than twice the highest frequency of interest.
The best implementation of the forced oscillation technique requires careful construction of the perturbation signal. This is the flow to be applied to the lungs, and the preferred approach for its constructing is to use composite signals consisting of sums of sine waves; thus,
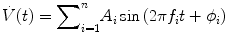
The frequencies (f i ) of the sine waves are distributed across frequency range of interest. The amplitudes (A i ) of the sine waves are chosen to give good signal to noise at each frequency of interest (e.g., constant). The phases (φ i ) of the sine waves may be chosen randomly. For example, the sine waves can be selected to try to minimize the peak–peak excursions in the final flow signal.
11.5.5.5 Passive Flow–Volume Technique
The passive flow–volume technique involves invoking the Hering–Breuer inflation reflex to relax the respiratory muscles at the end-inspiration after occlusion of the airway (LeSouef et al. 1984). Pressure is measured during this occlusion and the resultant flow–volume relationship during passive expiration is examined. The slope of the flow–volume relationship during passive expiration is examined. The slope of the flow–volume profile during expiration is the expiratory time constant (τ exp), and the extrapolation of this slope to zero flow allows the estimation of the FRC. Compliance is calculated from the ratio of the volume above FRC, at which the occlusion was made, to the end-inspiratory recoil pressure at this volume. Resistance is then calculated by relating (τ exp) to the measured compliance (τ exp = RC; R = τ exp/C). This assumes a linear relationship over the volume range measured and the inactivity of respiratory muscles during expiration. This assumption is obviously fulfilled when performed in paralyzed subjects; however, the resistive properties of the endotracheal tube may affect the shape of the flow–volume curve especially when a small endotracheal tube is used in infants (Brown et al. 1989).
11.5.5.6 Interrupter Technique
In order to partition respiratory resistance into components representing the conducting airways (R aw) and a peripheral phenomena representing the tissue viscoelastic components P dif, an interrupter technique with occlusion of the airway during expiration can be utilized (Sly and Bates 1988). When the airway is occluded during expiration, there is an initial rapid jump in pressure after occlusion (P int). A slower, secondary rise in pressure to a plateau occurs after occlusion (P dif). This component represents stress recovery within the tissues and the chest wall as well as any redistribution of gas (pendelluft) occurring between different lung units. Thus, this technique allows measurement of R aw (airway resistance including endotracheal tube and chest wall resistance), static elastance, and the viscoelastic properties of the lung from each occlusion. It is important to note that respiratory muscle activity may affect the accuracy of these measurements.
11.5.6 Respiratory Mechanics by Least-Squares Fitting
The single-compartment model of the respiratory system captures the essential mechanical feature of the respiratory system; it can be inflated and deflated to mimic breathing. This model has a single mechanical freedom because its state is completely defined by its compartmental volume. Figure 11.8 illustrates a single-compartment linear model. In this model by choosing the dimensions of the conduit appropriately, we can give it a resistance similar to any particular set of pulmonary airways. By choosing the stiffness of the spring appropriately, we can give the compartment an elastance similar to that of a real lung. Utilizing fitting models to data by least squares, we can make the single-compartment linear model behave like a real respiratory system. If the model were to be driven by the same flow signal as the real system, it would require a pressure signal that is similar to that applied to the real system. This is achieved by choosing appropriate values for the model parameters resistance (R), elastic (E), resting pressure (P 0). The values chosen are required that the behavior of the model matches that of the real system in the “least-squares sense.” Fortunately, for the single-compartment linear model, this can be done by multiple linear regressions.
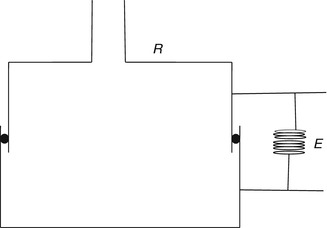

Fig. 11.8
Single-compartment linear model. R is the resistance of conduit and E is elastance illustrated as a spring. The stiffness of the spring offers an elastance similar to the lung. In this model R is resistance and is controlled by choosing the dimensions of the conduit. E is elastance and is determined by the stiffness of the spring
The least-squares regression method of measuring resistance involves relating the driving pressure of the system (P dr) to the corresponding flow (Mortola et al. 1982). Driving pressure is corrected by subtracting the contribution of the elastic and viscoelastic pressure components from transpulmonary pressure (P tp). Then P dr is plotted against flow, and linear regression is used to determine the slope that is the resistance of the system. This technique also assumes a linear relationship of the data. Most physical systems will exhibit approximately linear behavior provided they operate within a sufficiently modest amplitude range. When a system is forced to operate over a large amplitude range, its behavior often becomes highly nonlinear.
Least mean squares analysis minimizes the mean squared error between the measured pressure and the calculated pressure for each sampled point using a particular equation. Multiple linear regressions allow multiple independent variables to be simultaneously included in the regression calculation.
11.5.7 Practical Application and Result Interpretation
Measurement of respiratory mechanics in a relaxed ventilated patient can be obtained using the technique of rapid airway occlusion during constant flow inflation (Rossi et al. 1985a). Rapid airway occlusion at the end of a passive inflation produces an immediate drop in both airway pressure (P aw) and transpulmonary pressure (P l) from a peak value (P peak) to a lower initial value (P init) followed by a gradual decrease until a plateau (P plat) is achieved after 3–5 s (Rossi et al. 1985b) (Fig. 11.9). P init is measured by back extrapolation of the slope of the latter part of the pressure tracing to the time of the airway occlusion. P plat on the P aw, P l, and pleural pressure (P es) tracings represent the static end-inspiratory recoil pressure of the total respiratory system, lung, and chest wall, respectively.
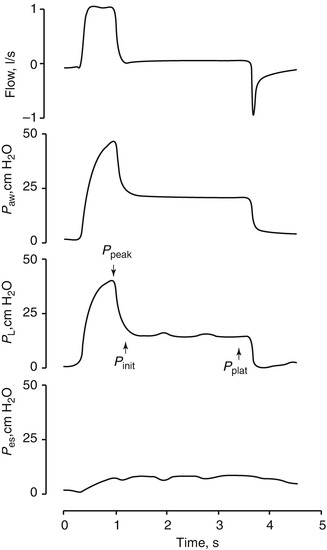

Fig. 11.9
Flow (inspiration upward), P aw, P l, and P es tracings in a representative patient during passive ventilation. An end-inspiratory occlusion produced a rapid decline in both P aw and P l from P peak to a lower P init, followed by gradual decrease to P plat (From Jubran and Tobin (1997))
11.5.7.1 Elastance/Static Compliance
Total static compliance of the respiratory system (C st,tot) is frequently measured and monitored during mechanical ventilation. Total static compliance is the pressure to overcome the elastic forces of the respiratory system for a given tidal volume and under a zero flow (static) condition. The end-inspiratory airway occlusion method is clinically used to measure static compliance of the respiratory system or its reciprocal, elastance of the respirator system (E st,rs), according to the following equation (Foti et al. 1997):
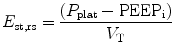 where P plat is plateau pressure obtained after occluding the airway. PEEPi is intrinsic PEEP and V T is tidal volume. Using an esophageal balloon catheter, E st,rs can be partitioned into its lung and chest wall components by dividing (P plat−PEEPi) by V T on the P l and P es tracings, respectively.
where P plat is plateau pressure obtained after occluding the airway. PEEPi is intrinsic PEEP and V T is tidal volume. Using an esophageal balloon catheter, E st,rs can be partitioned into its lung and chest wall components by dividing (P plat−PEEPi) by V T on the P l and P es tracings, respectively.
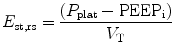
Specific measuring conditions must be met for a valid static compliance value including passive tidal volume (inspiration and expiration) and compressible volume correction for tubing; the plateau must have an end-inspiratory pause of at least 1 s with a stable pressure within 0.5 cm H2O over 2 readings at least 10 ms apart.
Changes in static compliance are associated with changes in lung elasticity; lung pathology that increases lung recoil or decreases lung volume will decrease the static compliance.
11.5.7.2 Dynamic Compliance
Formerly known as the effective dynamic compliance, the dynamic characteristics (DynChar) can be derived by dividing the ventilator delivered V T by (peak P aw – PEEP). Since the relationship of volume versus pressure during a dynamic event is subject to resistive forces inside the system, it is not considered a measure of dynamic compliance.
Total dynamic characteristics describe the components of total lung or parenchymal compliance plus the pressure required to overcome the airway resistance in the delivery of a tidal volume. Dynamic characteristics thus reflect resistive and elastic properties of the respiratory system. It is the tidal volume relative to the peak airway pressure under a dynamic condition and is expressed by the following relation:
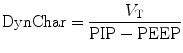
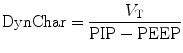
Trended values are thus clinically helpful reflecting resistive and elastic properties of the respiratory system.
Figure 11.10 is a volume–pressure loop from a constant flow mode of ventilation. The slope of AC reflects the total dynamic characteristics of the respiratory system.
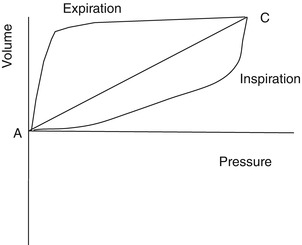

Fig. 11.10
Volume–pressure loop from a constant flow mode of ventilation. The slope of AC reflects the total dynamic characteristics of the respiratory system. Pressure–volume loop of patient’s lung with acute respiratory distress syndrome
The difference between static compliance and dynamic characteristics can be used as an indirect index of flow-resistive properties of the respiratory system.
Alternatively, dynamic elastance of the respiratory system (E dyn,rs) can be obtained by dividing the difference in P aw at points of zero flow by delivered V T (Nicolai et al. 1993). Accordingly, E dyn,rs can be computed according to the formula:
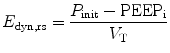 E dyn,rs can be partitioned into its lung (E dyn,L) and chest wall components by dividing (P init − PEEPi) pm P l and P es tracings.
E dyn,rs can be partitioned into its lung (E dyn,L) and chest wall components by dividing (P init − PEEPi) pm P l and P es tracings.
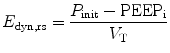
11.5.7.3 Pressure–Volume Curves
A pressure–volume curve of the respiratory system can be constructed in a paralyzed patient by measuring the airway pressure as the lungs are progressively inflated with a 1.5–2 l syringe. A lower inflection point and an upper inflection point may be seen on the pressure–volume curve (Fig. 11.11) (Mergoni et al. 2001). A lower inflection point is thought to reflect the point at which small airways and alveoli reopen, corresponding to closing volume. It has been recommended that the PEEP level should be set slightly above this closing volume (Mergoni et al. 2001).
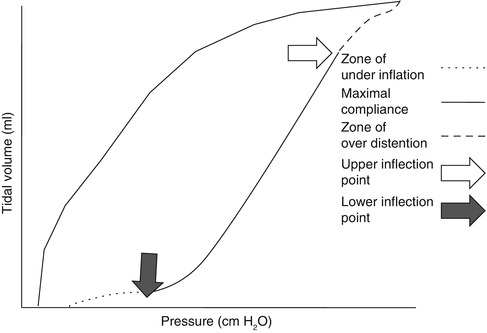

Fig. 11.11
In this loop airway pressure continues to increase beyond the zone of maximal compliance, and the inspiratory limb flattens into the zone of overdistension (dashed line). This portion of the curve represents alveolar overdistension and decreased compliance. The point at which this occurs is called the upper inflection point (UIP). The airway pressure at the upper inflection point identifies the pressure beyond which alveolar overdistension occurs
11.5.7.4 Resistance
Airway resistance can be measured in ventilator patients by using the technique of rapid airway occlusion during constant flow inflation (Polese et al. 1991). This technique implies that flow is interrupted at the end of inspiration while pressure is kept constant during a period of time (pause time). The interrupter technique is only valid when the ventilator operates in a constant flow mode that means that flow is constant throughout inspiration. Resistance in mechanical ventilation describes the airflow condition during both inspiration and expiration. Resistance represents the flow-resistive elements of the respiratory system. It is expressed as a pressure variation over gas flow using the following general equation:
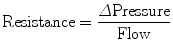
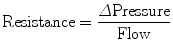
By substituting standard units, it becomes
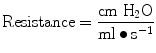
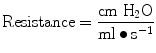
Airway resistance is affected by flow, tidal volume, and the network dimensions. The size of the endotracheal tube is an important element in gas flow through the breathing circuit and thus affects resistance. When delivering a set tidal volume at a set flow, smaller and longer tubes will produce larger resistance to gas flow.
When a ventilator operates in a constant flow mode, the resistive elements of the respiratory system/breathing circuit can be visualized and calculated with the pressure–time waveform (Fig. 11.12). The pressure–time waveform begins with an exponential rise to peak inspiratory pressure.
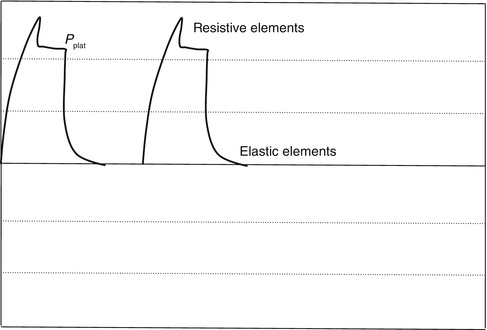

Fig. 11.12
When a ventilator operates in a constant flow mode, the resistive elements of the respiratory system/breathing circuit can be visualized and calculated with the pressure–time waveform
The first step is a function of flow and resistance during the initial portion of inspiration. The higher the step, the larger the resistance. The second portion of the waveform is a linear increase to peak inspiratory pressure and is a function of flow being constant throughout inspiration. This second portion represents the elastic properties of the respiratory system.
As peak inspiratory pressure is reached, a pause time or plateau is maintained, while pressure inside the airways and the breathing circuit equilibrates at plateau pressure (P plat). Flow then stops while pressure equilibrates.
Figure 11.12 is a pressure–time waveform from a constant flow mode of ventilation and illustrates various elements related to resistive and elastic properties of the respiratory system.
Inspiratory resistance is the difference between PIP and P plat over flow value at PIP, as expressed by the following equation:
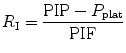
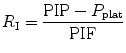
Expiratory resistance is the difference between P plat and total PEEP over flow value at the onset of exhalation, as expressed by the following equation:


11.5.7.4.1 Limitations
Specific measuring conditions must be met for a valid inspiratory and expiratory resistance value which includes a passive tidal volume (inspiration and expiration) and constant flow over a fixed inspiratory time for inspiratory resistance only; the P plat must have an end-inspiratory pause of at least 1 s with a stable pressure within 0.5 cmH2O over 2 readings at least 10 ms apart.
11.6 Respiratory Time Constants
11.6.1 Time Constants: Basic Meaning and Concepts of Intrapulmonary Pressure Equilibration
The time constant of the lung (TC) is a concept borrowed from electrical engineering that describes the phenomenon whereby a given percentage of a passively exhaled breath of air will require a constant amount of time to be exhaled regardless of the starting volume given constant lung mechanics. Exponential functions are often described with time constants, designated by the Greek letter τ (tau). The time constant characterizes the rate of variation of the function over a period of time. Short time constants imply a fast rate of change and, vice versa, long time constant implies a slow rate of change.
During quiet breathing, equilibration between alveolar and mouth pressures occur at both the end of expiration and the end of inspiration such that time constants of the respiratory units are relatively small (0.01 s). Therefore, during quiet breathing the change in volume divided by the change in pleural pressure is dynamic compliance of the respiratory system and is the same as the static compliance. In the normal lung, since the time constants are small and equilibration between alveolar and mouth pressure still occurs, increases in breathing frequency to rates of 80/min do not affect the measured compliance. In contrast, in patients with peripheral airway disease, with more rapid breathing, the time constants of at least some of the respiratory units are increased so that equilibration between the alveolar and mouth pressure does not occur at either end-inspiration or end-expiration. Accordingly, the volume change with a given pleural pressure change falls with increasing respiratory rate, and the compliance is said to be frequency dependent (Woodcock et al. 1969).
Changes in dynamic compliance with increasing respiratory rate in patients with relatively normal expiratory flow rates may be marked. Woodcock et al. (1969) found that the dynamic compliance was reduced to less than 50 % of static compliance in mild asthmatics breathing at a respiratory frequency of 80/min. A large proportion of the decrease in dynamic compliance owes to the pendelluft effect where at times of zero flow at the mouth, air flows from one region to another. This mechanism is illustrated in Fig. 11.13. During inspiration, alveolus 1 fills more rapidly than alveolus 2 because of the increased airway resistance of the airways leading to alveolus 2 and hence its larger time constant. If the inspiratory time is short, alveolus 2 never becomes completely filled. Then on expiration, the pressure in alveolus 1 is higher than the pressure in alveolus 2 because of its larger volume; therefore, flow goes not only from alveolus 1 to the mouth but also from alveolus 1 to alveolus 2. The higher the frequency, the lower the tidal volume to the abnormal region.

Fig. 11.13
Effects of uneven time constants on ventilation. The airway leading to unit 2 is partially obstructed and therefore unit 2 has a longer time constant. After a slow expiration (a), the units have the same size. With a rapid inspiration (b), unit 1 fills more than unit 2 because it has a faster time constant. Shortly after the start of a rapid expiration (c), air moves not only from unit 1 to the airway opening but also from unit 1 to unit 2 because the pressure in unit 2 is less than pressure in unit 1. During the later phases of expiration (d), flow moves from unit 2 to unit 1. As the respiratory rate is progressively increased, the tidal volume of the abnormal region becomes smaller and smaller
Tests of dynamic compliance are sensitive indicators of peripheral airway disease. The time constants of the lung units distal to airway 2 mm in diameter are on the order of 0.01 s. Fourfold increase in some time constants is necessary to cause dynamic compliance to become frequency dependent.
Time constants of the respiratory units markedly influence the distribution of ventilation. A second factor that is influential is the regional differences in pleural pressures. Owing to the regional differences in pleural pressure, dependent parts of the lung are ventilated better. Other factors that influence the distribution of ventilation are the interdependence that exists between adjacent lung units and the presence of collateral pathways for ventilation.
11.6.1.1 Concepts of Intrapulmonary Pressure Equilibration
A model can be constructed in which the alveoli are represented by an elastic sac and the intrathoracic airways by a compressible tube, both of which are enclosed within a pleural space. The concept of an equal pressure point (EPP) described by Mead is when sufficient expiratory effort is generated then the pleural pressure becomes positive, and in this situation the intrabronchial pressure at some point along the airways is equal to the pleural pressure extrabronchial pressure. The EPP divides the airways into two components arranged in series with an upstream segment from the alveoli to the equal pressure point, where the distending pressure of the bronchi is positive, and a downstream segment from the EPP to the airway opening, where the distending pressure of the bronchi intrathoracic is negative. In these downstream segments collapse will occur during forced expiration.
There is no EPP when the pleural pressure is subatmospheric. However, when the pleural pressure becomes atmospheric, the EPP is at the airway opening. The EPP moves upstream as the pleural pressure becomes more positive. The alveolar pressure minus the pleural pressure represents the pressure drop from the alveolus to the EPP. This pressure represents the elastic recoil pressure of the lung. The resistance of the upstream segment is designated Rus. Therefore, flow is
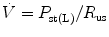 P st(L) is constant at a constant lung volume. Thus,
P st(L) is constant at a constant lung volume. Thus, 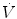 can only increase if R us decreases, which can be accomplished by moving the EPP upstream. The movement of the EPP upstream is caused by more and more effort until the pleural pressure reaches a level at which further increases in it do not lead to further increase in
can only increase if R us decreases, which can be accomplished by moving the EPP upstream. The movement of the EPP upstream is caused by more and more effort until the pleural pressure reaches a level at which further increases in it do not lead to further increase in 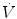 . This lack of change in flow is called
. This lack of change in flow is called 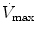 and corresponds to point on pressure–flow curve where the waveform is flat.
and corresponds to point on pressure–flow curve where the waveform is flat.
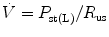
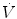 can only increase if R us decreases, which can be accomplished by moving the EPP upstream. The movement of the EPP upstream is caused by more and more effort until the pleural pressure reaches a level at which further increases in it do not lead to further increase in
can only increase if R us decreases, which can be accomplished by moving the EPP upstream. The movement of the EPP upstream is caused by more and more effort until the pleural pressure reaches a level at which further increases in it do not lead to further increase in 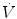 . This lack of change in flow is called
. This lack of change in flow is called 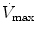 and corresponds to point on pressure–flow curve where the waveform is flat.
and corresponds to point on pressure–flow curve where the waveform is flat.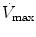 is dependent on two factors:
is dependent on two factors: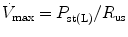
 a decrease in elastic recoil of the lung is just as important as is increased airway resistance.
a decrease in elastic recoil of the lung is just as important as is increased airway resistance.Figure 11.14 represents a model described by Pride (Pride et al. 1967) where the airways are divided into two rigid tubes connected in series by a short segment of a collapsible tube. The airways are divided into an upstream segment between the alveoli and airways into an upstream segment between the alveoli and the distal end of the collapsible segment to the airway opening. They defined the critical closing pressure of the collapsible segment (P′tm) as the transmural pressure (P tm), at which the segment collapsed. Thus, the transmural pressure, in this distensible object, is the pressure inside the wall minus the pressure outside the wall. The value of P′tm represents the necessary distending pressure to maintain the collapsible segment patent. So this segment would be fully open when the distending pressure exceeds P′tm and fully collapsed when P tm fell below P′tm. Calculation of the transmural pressure in the collapsible segment is
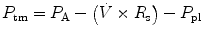 where R s is the resistance of the segment upstream from the collapsible segment. Since
where R s is the resistance of the segment upstream from the collapsible segment. Since
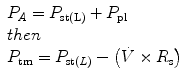
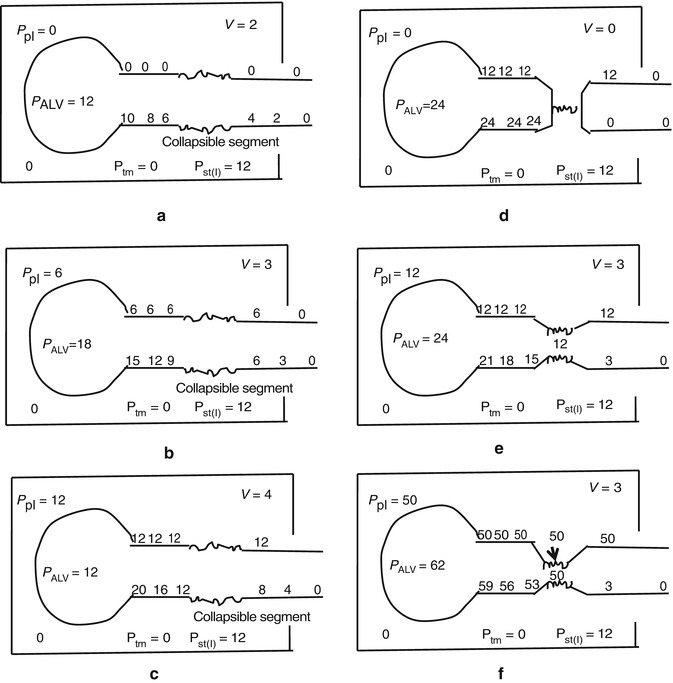
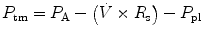

Fig. 11.14
A schematic representation of the collapsible-segment concept. In these diagrams the lung volume is that giving a P st(I) of 12 and it is assumed that P′tm is zero. (a) Pressure along the airways when P tm still exceeds P′tm. There is no collapse. (b) Pressure along the airways when P tm approaches P′tm. Note that the flow rate increases from (a). (c) Pressures along the airways when pleural pressures are increased more. Note that P tm at the collapsed segment is now 8 − 12 = −4 which is below P′tm = 0, so this higher flow is impossible since the collapsible segment must collapse. (d) Pressures along the airways when there is no flow. Now P tm is 24 − 12 = 12, so the airway must open. (e) Pressure along the airways when the collapsible segment is partially collapsed such tat P tm = P′tm. (f) Pressures along the airways when the collapsible segment is partially collapsed such that P tm = P′tm. (f) Pressures along the airways when the alveolar pressure is raised much higher. Note that the collapsible segment is more collapsed than in (e) and that the flows in (b, e, and f) are also identical. The airway pressures downstream from the collapsible segment in (b, e, and f) are also identical
Therefore, as 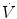 increases, P tm decreases. When
increases, P tm decreases. When 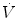 increases to a critical level (
increases to a critical level (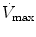 ), P tm drops to P′tm. This is demonstrated in Fig. 11.14 where P tm = 6 − 6 = 0 and it is assumed P′tm = 0. If flow rates increase more, as seen in Fig. 11.14, the P tm would fall below P′tm and there would be no flow due to the collapse of the segment (Fig. 11.14d). However, in this situation the intrabronchial pressure becomes the same as the alveolar pressure, due to the absence of flow, and P tm would exceed P′tm and flow would resume. If the collapsible segment opens all the way,
), P tm drops to P′tm. This is demonstrated in Fig. 11.14 where P tm = 6 − 6 = 0 and it is assumed P′tm = 0. If flow rates increase more, as seen in Fig. 11.14, the P tm would fall below P′tm and there would be no flow due to the collapse of the segment (Fig. 11.14d). However, in this situation the intrabronchial pressure becomes the same as the alveolar pressure, due to the absence of flow, and P tm would exceed P′tm and flow would resume. If the collapsible segment opens all the way, 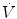 again exceeds
again exceeds 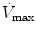 , P tm falls below P′tm and airflow ceases. Thus, the best way to explain this interrelationship is to consider the collapsible segment as a variable resistor illustrated in Fig. 11.14e, f. Partial collapse of the segment occurs when pleural pressure is reached to level necessary to cause collapse with P tm equal to P′tm. While pleural pressure increases further, there is a corresponding pressure drop across the collapsible segment. So as can be seen in Fig. 11.14b, e, f, once flow limitation is met, flow and intrabronchial pressure downstream do not change. If we examine this from our mathematical model, we recognize that flow limitation occurs when P tm = P′tm. If we substitute P tm’s for P tm in our previous equation, then
, P tm falls below P′tm and airflow ceases. Thus, the best way to explain this interrelationship is to consider the collapsible segment as a variable resistor illustrated in Fig. 11.14e, f. Partial collapse of the segment occurs when pleural pressure is reached to level necessary to cause collapse with P tm equal to P′tm. While pleural pressure increases further, there is a corresponding pressure drop across the collapsible segment. So as can be seen in Fig. 11.14b, e, f, once flow limitation is met, flow and intrabronchial pressure downstream do not change. If we examine this from our mathematical model, we recognize that flow limitation occurs when P tm = P′tm. If we substitute P tm’s for P tm in our previous equation, then
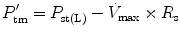 or can be rewritten to calculate maximum flow as
or can be rewritten to calculate maximum flow as
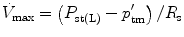
 increases, P tm decreases. When
increases, P tm decreases. When  increases to a critical level (
increases to a critical level (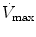 ), P tm drops to P′tm. This is demonstrated in Fig. 11.14 where P tm = 6 − 6 = 0 and it is assumed P′tm = 0. If flow rates increase more, as seen in Fig. 11.14, the P tm would fall below P′tm and there would be no flow due to the collapse of the segment (Fig. 11.14d). However, in this situation the intrabronchial pressure becomes the same as the alveolar pressure, due to the absence of flow, and P tm would exceed P′tm and flow would resume. If the collapsible segment opens all the way,
), P tm drops to P′tm. This is demonstrated in Fig. 11.14 where P tm = 6 − 6 = 0 and it is assumed P′tm = 0. If flow rates increase more, as seen in Fig. 11.14, the P tm would fall below P′tm and there would be no flow due to the collapse of the segment (Fig. 11.14d). However, in this situation the intrabronchial pressure becomes the same as the alveolar pressure, due to the absence of flow, and P tm would exceed P′tm and flow would resume. If the collapsible segment opens all the way, 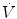 again exceeds
again exceeds 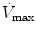 , P tm falls below P′tm and airflow ceases. Thus, the best way to explain this interrelationship is to consider the collapsible segment as a variable resistor illustrated in Fig. 11.14e, f. Partial collapse of the segment occurs when pleural pressure is reached to level necessary to cause collapse with P tm equal to P′tm. While pleural pressure increases further, there is a corresponding pressure drop across the collapsible segment. So as can be seen in Fig. 11.14b, e, f, once flow limitation is met, flow and intrabronchial pressure downstream do not change. If we examine this from our mathematical model, we recognize that flow limitation occurs when P tm = P′tm. If we substitute P tm’s for P tm in our previous equation, then
, P tm falls below P′tm and airflow ceases. Thus, the best way to explain this interrelationship is to consider the collapsible segment as a variable resistor illustrated in Fig. 11.14e, f. Partial collapse of the segment occurs when pleural pressure is reached to level necessary to cause collapse with P tm equal to P′tm. While pleural pressure increases further, there is a corresponding pressure drop across the collapsible segment. So as can be seen in Fig. 11.14b, e, f, once flow limitation is met, flow and intrabronchial pressure downstream do not change. If we examine this from our mathematical model, we recognize that flow limitation occurs when P tm = P′tm. If we substitute P tm’s for P tm in our previous equation, then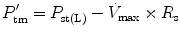
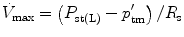
Thus, 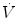 max depend upon three different factors: (1) the resistance of the upstream segment (R s), (2) the elastic recoil of the lung (R st(L)), and (3) the tendency of the airways to collapse (P′tm). Clinical examples of this relationship with reduced flow rate during expiration can be seen in asthma with constriction of the bronchial smooth muscles increasing the tendency of the airways to collapse (P′tm) and thereby reduce flow rates, and the lungs cannot empty to a lung volume below which P′tm exceeds P st(L).
max depend upon three different factors: (1) the resistance of the upstream segment (R s), (2) the elastic recoil of the lung (R st(L)), and (3) the tendency of the airways to collapse (P′tm). Clinical examples of this relationship with reduced flow rate during expiration can be seen in asthma with constriction of the bronchial smooth muscles increasing the tendency of the airways to collapse (P′tm) and thereby reduce flow rates, and the lungs cannot empty to a lung volume below which P′tm exceeds P st(L).
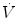 max depend upon three different factors: (1) the resistance of the upstream segment (R s), (2) the elastic recoil of the lung (R st(L)), and (3) the tendency of the airways to collapse (P′tm). Clinical examples of this relationship with reduced flow rate during expiration can be seen in asthma with constriction of the bronchial smooth muscles increasing the tendency of the airways to collapse (P′tm) and thereby reduce flow rates, and the lungs cannot empty to a lung volume below which P′tm exceeds P st(L).
max depend upon three different factors: (1) the resistance of the upstream segment (R s), (2) the elastic recoil of the lung (R st(L)), and (3) the tendency of the airways to collapse (P′tm). Clinical examples of this relationship with reduced flow rate during expiration can be seen in asthma with constriction of the bronchial smooth muscles increasing the tendency of the airways to collapse (P′tm) and thereby reduce flow rates, and the lungs cannot empty to a lung volume below which P′tm exceeds P st(L).11.6.2 Measurement of the Time Constant
The pressure applied by the ventilator and the respiratory muscles is necessary to overcome the extrinsic and intrinsic forces on the lungs and chest wall during ventilation in intubated patients.
Theoretically, inspiratory volume production is active and can be forced by external pressure application; but since exhalation is passive, it cannot. Thus, time is required to empty the lungs and that time depends on the expiratory time constant.
Expiratory time constant is defined as the product of the total respiratory system compliance and the total expiratory resistance. While the former is determined by factors internal to the subject, the latter is the sum of airway resistance, any viscous tissues resistance, and externally applied resistance, such as valves and hoses in intubated patients. The calculation of the expiratory time constant requires knowledge about all of these elements and thus the measurement of flow and pressure at the airway opening.
The actual expiratory time constant can be calculated as (Brunner et al. 1995)
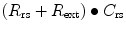 R rs is the resistance of the respiratory system, R ext the resistance of the expiratory valve and circuit, and C rs the compliance of the total respiratory system. The expiratory resistance of the ventilator, R ext, can be measured separately by dividing the pressure drop with a flow rate directed through the expiratory valve and hoses: (R ext = AP/AV prime).
R rs is the resistance of the respiratory system, R ext the resistance of the expiratory valve and circuit, and C rs the compliance of the total respiratory system. The expiratory resistance of the ventilator, R ext, can be measured separately by dividing the pressure drop with a flow rate directed through the expiratory valve and hoses: (R ext = AP/AV prime).
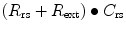
11.6.3 Simplified Approach (Analysis of the Flow–Time Curve and the Flow–Volume Loop)
11.6.3.1 Flow–Time Curve
In mechanical ventilation, for practical purposes, an event is considered complete after three time constants. For the adult respiratory system, the normal time constant is 0.79 s.
The actual value of one time constant is obtained through the product of compliance × resistance:
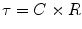
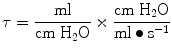
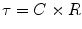
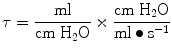
As an example, a system with a total lung/thorax static compliance of 60 ml/cm H2O, an expiratory resistance of 0.13 cm H2O/ml, and no auto-PEEP has a time constant τ of
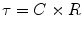
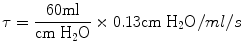
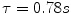
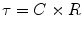
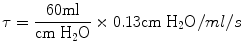
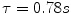
Figure 11.15 illustrates a flow–time waveform during a constant pressure mode of ventilation with a short and long time constant. In a decaying exponential function, a time constant of 0.78 s means that after one time constant (0.78 s) the value of the variable on the y-axis decreases to 37 % of its final value; after two time constants (1.56 s), it decreases to 13.5 % of its final value; and after three time constants (2.34 s), the value of the variable on the y-axis decreases to 5 % of its final value.
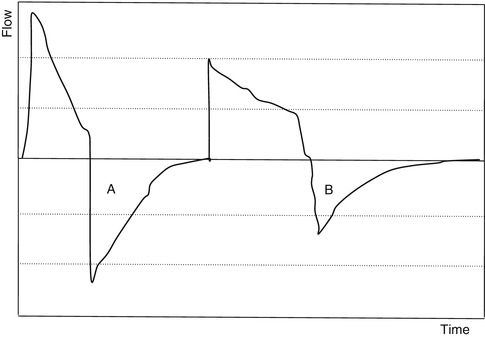

Fig. 11.15
Flow–time waveform from a constant pressure mode of ventilation. A represents an exponential function with a short time constant. B represents exponential function with a long time constant
In this example of a flow–time waveform from a constant flow mode of ventilation (Fig. 11.16), if the expiratory time is shorter than 2.34 s (3 × 0.78), air trapping will be present, causing auto-PEEP.
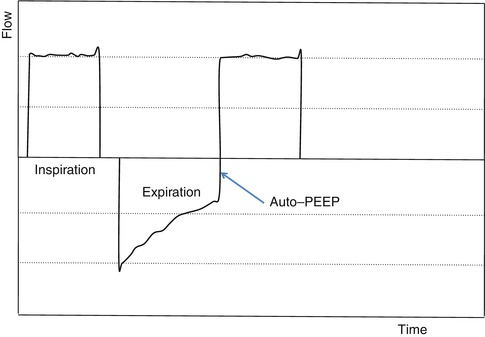

Fig. 11.16
Flow–time waveform from a constant flow mode of ventilation. Tracing reveals increased resistance with evidence seen with the linear decay during expiration with a slow decay to baseline with nonzero flow conditions at the end of expiration with evidence of auto-PEEP
To prevent auto-PEEP and air trapping, the expiratory time should always be longer than three time constants.
11.6.3.2 Flow–Volume Loop
The flow–volume loop (Fig. 11.17) has an inspiratory and expiratory phase. During the inspiratory phase, there is a rapid rise to peak inspiratory flow throughout inspiration with a rapid decay from peak inspiratory flow to baseline. In expiration there again is a rapid decay to peak expiratory flow, and then the flow progressively returns to baseline. During a constant flow mode of ventilation, resistive changes are not reflected in the inspiratory profile. An airflow limitation that is reflective of resistive changes is associated with a convex (to the volume axis) shape of the second phase of the expiratory profile of the loop. These changes are reflective of dynamic changes and no static characteristics of the respiratory system can described with a flow–volume loop.
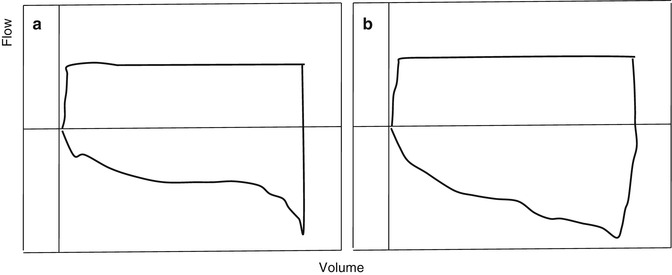

Fig. 11.17
Flow–volume loop from a constant flow mode of ventilation. Tracing (a) illustrates increased resistance and (b) normal resistance. In tracing (a) increased resistance can be seen with linear return to baseline
11.7 Lung Volume Measurements in the Ventilated Patient
11.7.1 Techniques and Methods
In order to use measurement of respiratory mechanics in clinical decision making for mechanically ventilated patients, some measurement of volume is required. Volume in mechanically ventilated patients can consist of the volume delivered by the ventilator or some measurement of the patient’s actual lung volume. The discussion below will first discuss measurement of volume by the ventilator and on methods of measuring the patient’s actual lung volumes.
11.7.1.1 Measurement of the Delivered Volume by the Mechanical Ventilator
Volume (V) can be obtained by numerically integrating flow 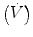 by a computer. The trapezoidal rule is sufficient for virtually all respiratory applications, provided
by a computer. The trapezoidal rule is sufficient for virtually all respiratory applications, provided 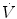 is sampled rapidly enough (50 Hz or more). Thus, this integration can be accomplished when
is sampled rapidly enough (50 Hz or more). Thus, this integration can be accomplished when
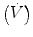 by a computer. The trapezoidal rule is sufficient for virtually all respiratory applications, provided
by a computer. The trapezoidal rule is sufficient for virtually all respiratory applications, provided 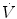 is sampled rapidly enough (50 Hz or more). Thus, this integration can be accomplished when
is sampled rapidly enough (50 Hz or more). Thus, this integration can be accomplished when